
21.(12分)古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有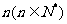 个圆盘依其半径大小,大的在下,小的在上套在
个圆盘依其半径大小,大的在下,小的在上套在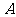 柱上,现要将套在
柱上,现要将套在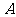 柱上的盘换到
柱上的盘换到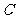 柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子
柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子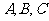 可供使用.
可供使用.
现用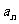 表示将
表示将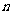 个圆盘全部从
个圆盘全部从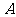 柱上移到
柱上移到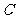 柱上所至少需要移动的次数,回答下列问题:
柱上所至少需要移动的次数,回答下列问题:
(1)写出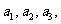 并求出
并求出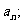
(2)记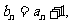 求和
求和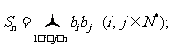
(其中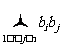 表示所有的积
表示所有的积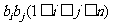 的和)
的和)
(3)证明:
20.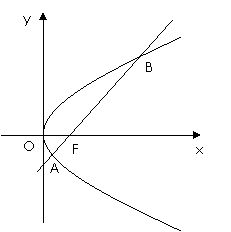 (12分)如图,斜率为1的直线过抛物线
(12分)如图,斜率为1的直线过抛物线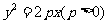 的焦点,与抛物线交于两点
的焦点,与抛物线交于两点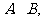
将直线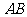 按向量
按向量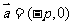 平移到直线
平移到直线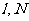 为
为 上的动点.
上的动点.
(1)若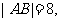 求抛物线的方程;
求抛物线的方程;
(2)求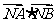 的最小值.
的最小值.
19.(12分)已知函数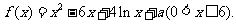
(1)求函数的单调区间;
(2)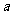 为何值时,方程
为何值时,方程 有三个不同的实根.
有三个不同的实根.
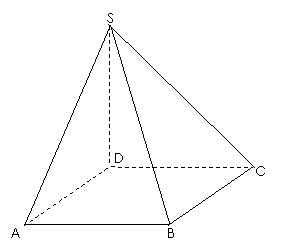
18.(13分)如图,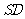 垂直于正方形
垂直于正方形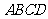 所在的平面,
所在的平面,
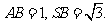
(1)求证: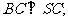
(2)设棱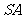 的中点为
的中点为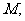 求异面直线
求异面直线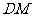 与
与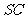 所成角的大小.
所成角的大小.
17.(13分)正项数列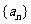 的前
的前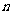 项和为
项和为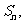 且
且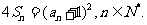
(1)试求数列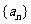 的通项公式;
的通项公式;
 (2)设
(2)设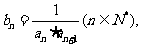 求数列
求数列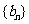 的前
的前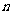 项和
项和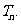
16.(13分)已知向量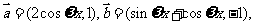
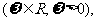
设函数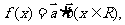 若
若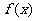 的最小正周期为
的最小正周期为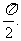
(1)求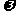 的值;
的值;
(2)求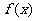 的单调区间.
的单调区间.
15.设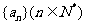 为等差数列,则使
为等差数列,则使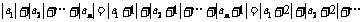
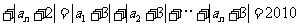 成立的数列
成立的数列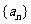 的项数
的项数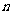 的最大值是__________.
的最大值是__________.
14.设函数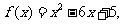 若实数
若实数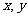 满足条件
满足条件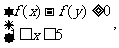 则
则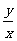 的最大值是_______.
的最大值是_______.
13.已知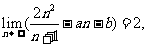 其中
其中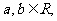 则
则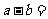 _____________.
_____________.
12.已知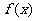 在
在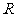 上是奇函数,且满足
上是奇函数,且满足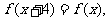 当
当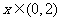 时,
时,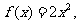 则
则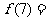
__________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com