
28.(2008安徽卷21).
设数列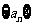 满足
满足 为实数
为实数 

(Ⅰ)证明: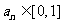 对任意
对任意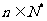 成立的充分必要条件是
成立的充分必要条件是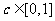 ;
;
(Ⅱ)设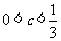 ,证明:
,证明: ;
;
(Ⅲ)设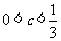 ,证明:
,证明:
解 (1) 必要性 :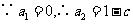 ,
,
又 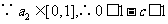 ,即
,即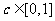
充分性 :设 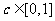 ,对
,对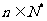 用数学归纳法证明
用数学归纳法证明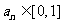
当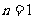 时,
时,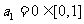 .假设
.假设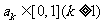
则 ,且
,且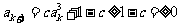
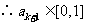 ,由数学归纳法知
,由数学归纳法知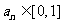 对所有
对所有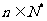 成立
成立
(2) 设 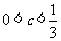 ,当
,当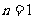 时,
时,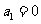 ,结论成立
,结论成立 

当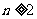 时,
时,
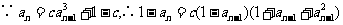
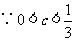 ,由(1)知
,由(1)知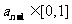 ,所以
,所以 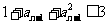 且
且 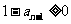
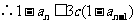
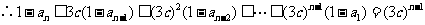
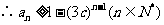
(3) 设 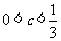 ,当
,当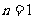 时,
时, ,结论成立
,结论成立
当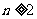 时,由(2)知
时,由(2)知
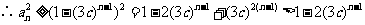
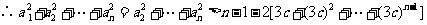


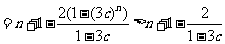
27.(2008江西)
数列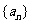 为等差数列,
为等差数列,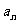 为正整数,其前
为正整数,其前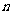 项和为
项和为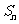 ,数列
,数列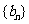 为等比数列,且
为等比数列,且 ,数列
,数列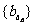 是公比为64的等比数列,
是公比为64的等比数列, .
.
(1)求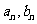 ;
;
(2)求证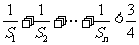 .
.
解:(1)设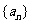 的公差为
的公差为 ,
,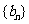 的公比为
的公比为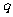 ,则
,则 为正整数,
为正整数,
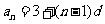 ,
,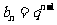
依题意有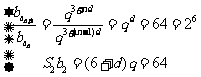 ①
① 

由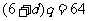 知
知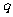 为正有理数,故
为正有理数,故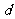 为
为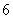 的因子
的因子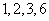 之一,
之一,
解①得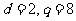
故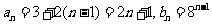
(2)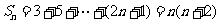
∴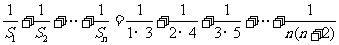

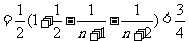
26.设数列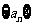 满足
满足 为实数
为实数
(Ⅰ)证明: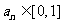 对任意
对任意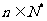 成立的充分必要条件是
成立的充分必要条件是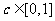 ;
;
(Ⅱ)设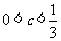 ,证明:
,证明: ;
;
(Ⅲ)设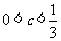 ,证明:
,证明:
解析: (1) 必要性 :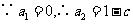 ,
, 

又 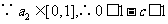 ,即
,即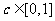
充分性 :设 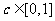 ,对
,对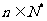 用数学归纳法证明
用数学归纳法证明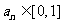
当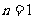 时,
时,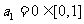 .假设
.假设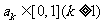
则 ,且
,且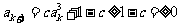
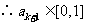 ,由数学归纳法知
,由数学归纳法知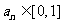 对所有
对所有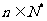 成立
成立
(2) 设 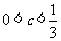 ,当
,当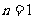 时,
时,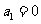 ,结论成立
,结论成立
当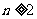 时,
时,
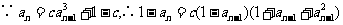
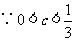 ,由(1)知
,由(1)知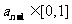 ,所以
,所以 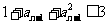 且
且 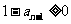
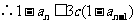
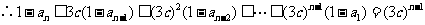
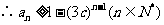
(3) 设 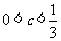 ,当
,当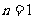 时,
时, ,结论成立
,结论成立
当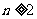 时,由(2)知
时,由(2)知
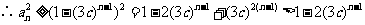
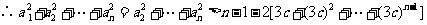
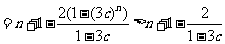


25.(2009湖北卷文)(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
解析:(1)如图,设矩形的另一边长为a m
则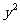 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=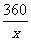 ,
, 

所以y=225x+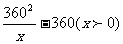
(II)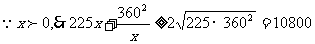

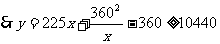 .当且仅当225x=
.当且仅当225x= 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
23.(2009年上海卷理)若行列式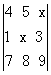 中,元素4的代数余子式大于0,
中,元素4的代数余子式大于0,
则x满足的条件是________________________ .


[答案]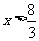
解析:依题意,得: (-1)2×(9x-24)>0,解得: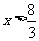
6.(2009山东卷文)某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
解析:设甲种设备需要生产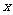 天, 乙种设备需要生产
天, 乙种设备需要生产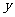 天, 该公司所需租赁费为
天, 该公司所需租赁费为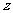 元,则
元,则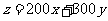 ,甲、乙两种设备生产A,B两类产品的情况为下表所示:
,甲、乙两种设备生产A,B两类产品的情况为下表所示:
 产品 产品 设备 |
A类产品 (件)(≥50) |
B类产品 (件)(≥140) |
租赁费 (元) |
|
甲设备 |
5 |
10 |
200 |
|
乙设备 |
6 |
20 |
300 |
则满足的关系为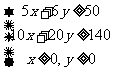 即:
即: ,
, 

作出不等式表示的平面区域,当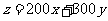 对应的直线过两直线
对应的直线过两直线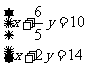 的交点(4,5)时,目标函数
的交点(4,5)时,目标函数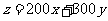 取得最低为2300元.
取得最低为2300元.
答案:2300
[命题立意]:本题是线性规划的实际应用问题,需要通过审题理解题意,找出各量之间的关系,最好是列成表格,找出线性约束条件,写出所研究的目标函数,通过数形结合解答问题..
22.(2009山东卷理)不等式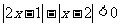 的解集为
.
的解集为
.
[解析]:原不等式等价于不等式组①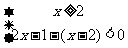 或②
或②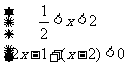
或③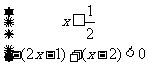 不等式组①无解,由②得
不等式组①无解,由②得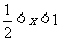 ,由③得
,由③得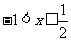 ,综上得
,综上得 ,所以原不等式的解集为
,所以原不等式的解集为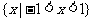 .
.
答案: 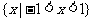


[命题立意]:本题考查了含有多个绝对值号的不等式的解法,需要根据绝对值的定义分段去掉绝对值号,最后把各种情况综合得出答案.本题涉及到分类讨论的数学思想.
21.(2009北京卷理)若实数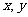 满足
满足 则
则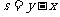 的最小值为__________.
的最小值为__________.
[答案]



解析:本题主要考查线性规划方面
的基础知. 属于基础知识、基本运算
的考查.
如图,当 时,
时,
 为最小值.
为最小值.
故应填 .
.
20.(2009上海卷文) 已知实数x、y满足 则目标函数z=x-2y的最小值是___________.
则目标函数z=x-2y的最小值是___________. 

[答案]-9
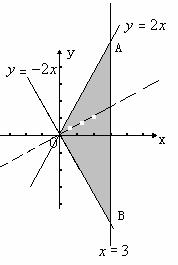
解析:画出满足不等式组的可行域如右图,目标函数化为: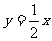 -z,画直线
-z,画直线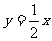 及其平行线,当此直线经过点A时,-z的值最大,z的值最小,A点坐标为(3,6),所以,z的最小值为:3-2×6=-9。
及其平行线,当此直线经过点A时,-z的值最大,z的值最小,A点坐标为(3,6),所以,z的最小值为:3-2×6=-9。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com