
6.数列{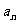 }中,a1=3,a2=7,当n≥l时,
}中,a1=3,a2=7,当n≥l时, 等于
等于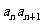 的个位数,则a2009等于
的个位数,则a2009等于
A.1 B.3 C.7 D.9
5.设向量a与b的夹角为θ,a=(2,1),a+2b=(4,5),则cosθ等于
A. B.
B.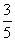 C.
C.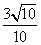 D.
D.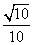
4.设p:f(x)=x3+2x2+mx+l在(-∞,+∞)内单调递增,q:m≥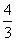 ,则p是q的
,则p是q的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.下列函数既是奇函数,又在区间[一1,1]上单调递减的是
A.f(x)=sinx B.f(x)=-|x+1|
C.f(x)=ln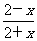 D.f(x)=
D.f(x)=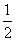 (
( )
)
2.函数y=ln(x-1)(x>2)的反函数是
A.y= +1(x>0)
B.y=
+1(x>0)
B.y= -1(x>0)
-1(x>0)
C.y= +1(x∈R) D.y=
+1(x∈R) D.y= -1(x∈R)
-1(x∈R)
1.集合M={x||x-3|≤4},N={y|y=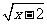 +
+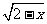 },则M∩N=
},则M∩N=
A.{0}
B.{2}
C.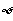 D.{x|2≤x≤7}
D.{x|2≤x≤7}
26.(本小题满分12分)
如图14,直线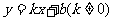 与坐标轴分别交于A、B两点,OA=8, OB=6.动点
与坐标轴分别交于A、B两点,OA=8, OB=6.动点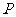 从
从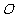 点出发,沿路线
点出发,沿路线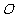 →
→ →
→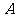 以每秒1个单位长度的速度运动,到达
以每秒1个单位长度的速度运动,到达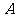 点时运动停止.
点时运动停止.
(1)直接写出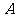 、
、 两点的坐标;
两点的坐标;
(2)求出直线AB的解析式;
(3)设点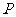 的运动时间为
的运动时间为 (秒),
(秒), 的面积为
的面积为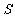 ,求
,求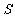 与
与 之间的函数关系式(不必写出自变量的取值范围);
之间的函数关系式(不必写出自变量的取值范围);
(4)当S=12时,直接写出点P的坐标,此时,在坐标轴上是否存在点M,使以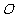 、
、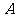 、
、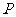 、
、 为顶点的四边形是梯形?若存在,请直接写出点
为顶点的四边形是梯形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

25.(本小题满分12分)
为加强对年满十八岁青年的公民意识、社会责任感和爱国主义的教育,某学校团组织在第六届成人节到来之际计划租用6辆客车送一批团员师生去天安门参加“五•一”升旗仪式.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车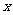 辆,租车总费用为
辆,租车总费用为 元.
元.
|
|
甲种客车 |
乙种客车 |
|
载客量(人/辆) |
45 |
30 |
|
租金(元/辆) |
280 |
200 |
(1)求出 (元)与
(元)与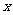 (辆)之间的函数关系式,指出自变量的取值范围;
(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?
24.(本小题满分10分)
如图13-1,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连结EB,过点A作AM BE,垂足为M,AM交BD于点F.
BE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图13-2,若点E在AC的延长线上,AM BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
 |
|||||
|
|||||
|
|||||

23.(本小题满分10分)
如图12,在由边长为1的小正方形组成的网格中,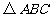 的三个顶点均在格点上,
的三个顶点均在格点上,
请按要求完成下列各题:
(1)画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 , AC的长为 ;
(3)请你在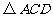 的三个内角中任选一个锐角,若你所选的锐角是
,则它所
的三个内角中任选一个锐角,若你所选的锐角是
,则它所
对应的正弦函数值是 ;
(4)若E为BC中点,F为AD中点.则tan∠CAE的值是 ,四边形AECF的形状
为 , 面积为 .

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com