
18.解:(1)由题意可知 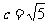 ,
,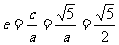 ,
,
∴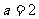 ,
,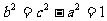 ,∴双曲线的标准方程为
,∴双曲线的标准方程为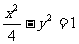 . …………3分
. …………3分
(2)设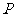 、
、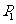 、
、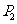 点的坐标分别为
点的坐标分别为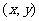 、
、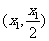 、
、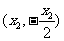 ,
,
由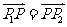 ,得
,得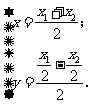 即
即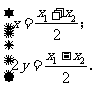 ………………………5分
………………………5分
将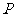 点坐标代入
点坐标代入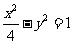 ,得
,得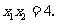 ……7分
……7分
设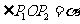 ,则
,则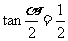 ,
,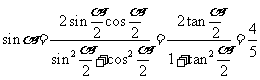 , ……9分
, ……9分
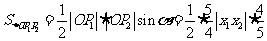 ,
,
将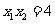 代入得
代入得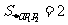 ……………………………………………………12分
……………………………………………………12分
由题意可知 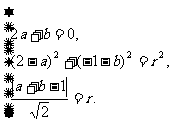 ………6分
………6分
解得  ………10分
………10分
∴圆C的方程为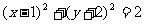 . ………12分
. ………12分
17.证明:(1)连结AC,设AC∩BD=O,连结EO,
∵四边形ABCD为矩形,∴O为AC的中点.
∴OE为△PAC的中位线. ∴PA∥OE,而OE 平面EDB,PA
平面EDB,PA 平面EBD,
平面EBD,
∴PA∥平面EDB. ……………6分
(2)∵PD⊥平面AC,BC 平面AC,∴BC⊥PD,而BC⊥CD,PD∩CD=D.
平面AC,∴BC⊥PD,而BC⊥CD,PD∩CD=D.
∴BC⊥平面PDC. ∵DE 平面PDC , ∴BC⊥DE . ①
平面PDC , ∴BC⊥DE . ①
又∵PD=DC, E是PC的中点, ∴DE⊥PC. ②
由①、②可知DE⊥平面PBC. ……………12分
14.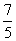 ; 15.①③
; 15.①③
21.(本小题满分14分)已知椭圆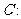
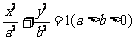 上存在一点
上存在一点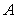 到椭圆左焦点的距离与到椭圆右准线的距离相等.
到椭圆左焦点的距离与到椭圆右准线的距离相等.
(1)求椭圆的离心率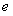 的取值范围;
的取值范围;
(2)若以椭圆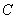 的两个焦点和短轴的两个端点为顶点的四边形是一个面积为2的正方形,求椭圆
的两个焦点和短轴的两个端点为顶点的四边形是一个面积为2的正方形,求椭圆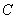 的方程;
的方程;
(3)在(2)的条件下,记椭圆的上顶点为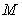 ,直线
,直线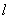 交椭圆于
交椭圆于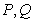 两点,问:是否存在直线
两点,问:是否存在直线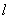 ,使椭圆右焦点
,使椭圆右焦点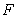 恰为
恰为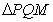 的垂心?若存在,求出直线
的垂心?若存在,求出直线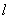 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

曾都一中2009-2010学年高二上学期期末考试文科数学 试题参考答案
试题参考答案
选择题答题栏
20.(本小题满分13分) 已知
已知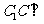 面
面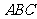 ,
,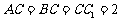 ,
,  ,点
,点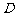 是
是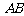 的中点,将
的中点,将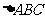 沿着
沿着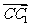 平移至
平移至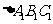 得下图.
得下图.
(1)求证: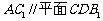 ;
;
 (2)求点
(2)求点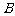 到
到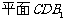 的距离;
的距离;
(3)求二面角 的大小的余弦值.
的大小的余弦值.
19.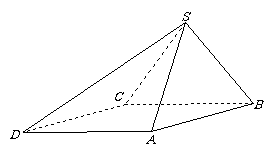 (本小题满分12分)如图,底面ABCD为平行四边形,点
(本小题满分12分)如图,底面ABCD为平行四边形,点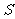 在面
在面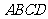 外,面
外,面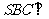 底面ABCD,已知
底面ABCD,已知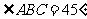 ,
,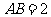 ,
,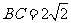 ,
,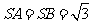 。
。
(1)求异面直线 所成角;
所成角;
(2)求直线SD与平面SBC所成角的正弦值。
18.(本小题满分12分) 已知双曲线的两个焦点的坐标为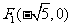 、
、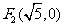 ,离心率
,离心率 .
.
(1)求双曲线的标准方程;(2)设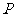 是(1)中所求双曲线上任意一点,过点
是(1)中所求双曲线上任意一点,过点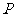 的直线与两渐近线
的直线与两渐近线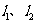 分别交于点
分别交于点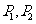 ,若
,若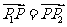 ,求
,求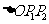 的面积.
的面积.
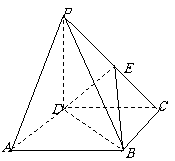
17.(本小题满分12分) 如图,四边形ABCD为矩形,PD⊥平
面ABCD,PD=DC,E是PC的中点.
(1)证明:PA∥平面EDB;(2)证明:DE⊥平面PBC.
16. (本小题满分12分)求经过点
(本小题满分12分)求经过点 ,圆心在直线
,圆心在直线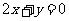 上,且和直线
上,且和直线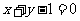 相切的圆的方程.
相切的圆的方程.
15.给出下列四个命题:①若动点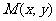 满足
满足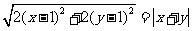 ,则动点
,则动点 的轨迹是抛物线;②经过两直线
的轨迹是抛物线;②经过两直线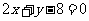 和
和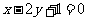 的交点且以
的交点且以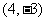 为方向向量的直线方程为
为方向向量的直线方程为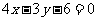 ;③若
;③若 直线
直线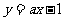 与焦点在x轴上的椭圆
与焦点在x轴上的椭圆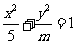 总有公共点,则
总有公共点,则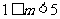 ;④动点P到定点(1,2)的距离与到定直线
;④动点P到定点(1,2)的距离与到定直线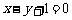 的距离相等的点的轨迹是一条抛物线。其中正确命题的序号是_______________ .
的距离相等的点的轨迹是一条抛物线。其中正确命题的序号是_______________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com