22．(本小题满分12分)

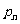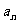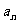已知点 (，)都在直线l：y＝2x+2上，P₁为直线l与x轴的交点，数列{}成等差数列，公差为1．(n∈N⁺)．

(Ⅰ)求数列{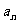}，{}的通项公式；

(Ⅱ)若f(n)＝问是否存在k∈N⁺,使得f (k+2011)＝2f(k)－2成立；若存在，求出k的值，若不存在，说明理由．

(Ⅲ)求证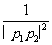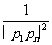：++…+＜(n≥2,n∈ N⁺)

21．(本小题满分12分)

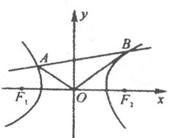
如图所示，F₁、F₂是双曲线x²－y²＝1的两个焦点，O为坐标原点，圆O是以F₁F₂为直径的圆，直线l：y＝kx+b与圆O相切，并与双曲线交于A、B两点．

(Ⅰ)根据条件求出b和k的关系式；

(Ⅱ)当(·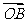)·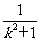＝m，且满足2≤m≤4时，求△AOB面积的取值范围．

20．(本小题满分12分)

　　 已知f(x)＝x³+mx²－x+2(m∈R)．

　 (Ⅰ)如果函数f(x)的单调递减区间为(－，1)，求函数f(x)的解析式；

　 (Ⅱ)若f(x)的导函数为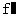(x)，对任意x∈(0，+∞)，不等式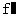(x)≥2xlnx－1恒成立，求实数m的取值范围．

19．(本小题满分12分)

　　 已知圆C：x²+y²－2x+4y－4＝0，是否存在斜率为1的直线l，使得l被圆C截得以弦AB为直径的圆经过原点?若存在，写出直线l的方程，若不存在，说明理由．

18．(本小题满分12分)

　　 在某社区举办的《2008奥运知识有奖问答比赛》中，甲、乙、丙三人同时回答一道有关奥运知识的问题，已知甲回答对这道题的概率是，甲、丙两人都回答错的概率是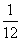，乙、丙两人都回答对的概率是．

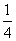　 (Ⅰ)求乙、丙两人各自回答对这道题的概率；

　 (Ⅱ)求答对该题的人数ξ的分布列的和Eξ

17．(本小题满分10分)

已知A、B、C是最大边长为2的△ABC的三个内角，m＝(2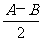sin，4sin)，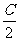

｜m｜＝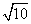

(Ⅰ)求tanA·tanB的值；

(Ⅱ)求tan∠C的最大值．

16．给出下列五个命题：

　　 ①存在α满足sinα+cosα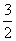＝；②y＝sin(－2x)是偶函数；③x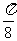＝是y＝sin(2x+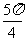)的一条对称轴；④y＝是以π为周期的(0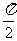，)上的增函数；⑤若α、β是第一象限的角，且α>β，则tanα>tanβ．其中正确命题的题号是________.

15．已知实数x、y满足,则x+2y的最大值是_______．

14．设F为抛物线y＝－x²的焦点，与抛物线相切于点P(－4，－4)的直线l与x轴的交点为Q，∠PQF＝__________．

13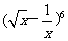．的展开式中，常数项为____________．(用数字作答)