
20.(本小题满分14分)已知数列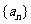 的通项公式为
的通项公式为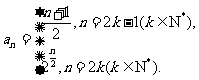 设
设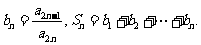
 (1)求
(1)求
(2)证明:当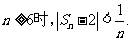
19.(本小题满分14分)
已知椭圆 的左右焦点分别为
的左右焦点分别为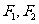 ,离心率
,离心率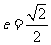 ,
,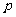 为椭圆上任一点,满足
为椭圆上任一点,满足 。
。
(1)求椭圆的标准方程;
(2)过点 的直线
的直线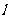 与该椭圆交于
与该椭圆交于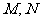 两点,且
两点,且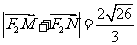 ,求直线
,求直线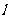 的方程。
的方程。
18.(本小题满分14分)
 如图,四边形
如图,四边形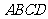 为矩形,且
为矩形,且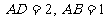 ,
, ,
, 为
为 上的动点.
上的动点.
(1) 当 为
为 的中点时,求证:
的中点时,求证: ;
;
(2) 设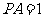 ,在线段
,在线段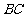 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角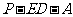 的大小为
的大小为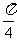 . 试确定点E的位置.
. 试确定点E的位置.
17.(本小题满分12分)
我校为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和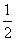 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数 的分布列与期望.
的分布列与期望.

16.(本小题满分12分)已知函数 是
是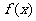 的导函数.
的导函数.
(1)求函数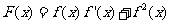 的最大值和最小正周期;
的最大值和最小正周期;
(2)若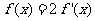 ,求
,求 的值.
的值.
(二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计算第一题的得分.
14. (坐标系与参数方程选做题)极坐标系中,曲线
(坐标系与参数方程选做题)极坐标系中,曲线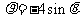 和
和 相交于点
相交于点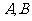 ,则
,则 =
.
=
.
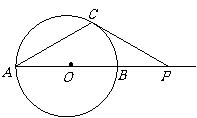
15. (几何证明选讲选做题)如图,⊙O的直径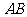 =6cm,
=6cm,
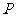 是
是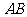 延长线上的一点,过
延长线上的一点,过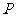 点作⊙O的切线,切点为
点作⊙O的切线,切点为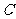 ,
,
连接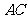 , 若
, 若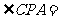 30°,PC =
cm。
30°,PC =
cm。
(一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须做答
9.一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人.为了调查职工的健康状况,用分层抽样的方法从全体职工中抽取一个容量为25的样本,应抽取超过45岁的职工 人.
10.设变量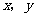 满足约束条件
满足约束条件 则
则 的最小值为 .
的最小值为 .
11. 若双曲线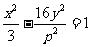 的左焦点在抛物线
的左焦点在抛物线 的准线上,则
的准线上,则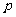 的值为 .
的值为 .
12.若⊙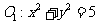 与⊙
与⊙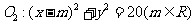 相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是
.
相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是
.

13.已知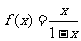 ,设
,设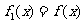 ,
,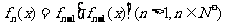 ,则
,则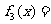 ,猜想
,猜想 .
.
8.定义域为R的函数f(x)满足f(x+2)=3f(x),当x∈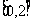 时,f(x)=x
时,f(x)=x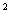 -2x,
-2x,
若x∈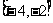 时,f(x)≥
时,f(x)≥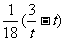 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.(-∞,-1]∪(0,3]
B.( -∞,- ]∪(0,
]∪(0,  ]
]
C.[-1,0)
∪[3,+∞)
D. [- ,0) ∪[
,0) ∪[ ,+∞)
,+∞)
7.已知抛物线 的焦点为
的焦点为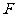 ,准线与
,准线与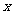 轴的交点为
轴的交点为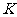 ,点
,点 在
在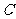 上且
上且 ,则
,则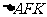 的面积为( )
的面积为( )
A.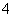 B.
B.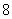 C.
C.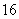 D.
D.
6.设 是两条不同的直线,
是两条不同的直线,  是两个不重合的平面,给定下列四个命题,其中为真命题的是(
)①
是两个不重合的平面,给定下列四个命题,其中为真命题的是(
)① 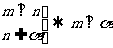 ②
② 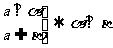 ③
③ 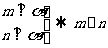 ④
④ 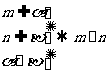
A. ①和② B. ②和③ C. ③和④ D. ①和④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com