
3.我国发射神舟号飞船时,先将飞船发送到一个椭圆轨道上,其近地点M距地面200km,远地点N距地面340km,进入该轨道正常运行时,其周期为T1,通过M、N点时的速率分别是V1、V2。当某次飞船通过N点时,地面指挥部发出指令,点燃飞船上的发动机,使飞船在短时间内加速后进入离地面340km的圆形轨道,开始绕地球做匀速圆周运动,周期为T2,这时飞船的速率为V3。比较飞船在M、N、P三点正常运行时(不包括点火加速阶段)的速率大小和加速度大小,及在两个轨道上运行的周期,下列结论正确的是( )
①.v1>v3 ②.v1>v2 ③.a2=a3 ④.T1> T2
A.①②③④ B.②③④ C.①③④ D.①②③
2.利用传感器和计算机可以研究快速变化的力的大小。实验时,把图甲中的小球举高到绳子的悬点O处,然后让小球自由下落,用这种方法获得弹性绳子的拉力随时间的变化如图乙所示,根据图象提供的信息,下列说法正确的是( )
A.t1、t2时刻小球的速度最大 B.t2、t5时刻小球的动能最小
C.t3、t4时刻小球的运动方向相同 D.t4与t3之差小于t7与t6之差


1. 如图所示,滑雪运动员由斜坡高速向下滑行时其速度-时间图象如图乙所示,则由图象中AB段曲线可知,运动员在此过程中( )
如图所示,滑雪运动员由斜坡高速向下滑行时其速度-时间图象如图乙所示,则由图象中AB段曲线可知,运动员在此过程中( )
A.机械能守恒
B.做变加速运动
C.做曲线运动
D.所受力的合力不断增大
9、解:(1) 又∵
又∵ 且
且 的最大值为1,∴
的最大值为1,∴ 由
由 ,故
,故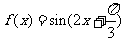 .
.
(2)由(1)知, 解得对称轴方程为:
解得对称轴方程为:
证: =
=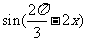
=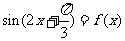 . ∴
. ∴ 是
是 的对称轴.
的对称轴.
注:也可通过 证得结论.
证得结论.
8、解:∵
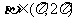 ,∴
,∴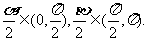 ∴
∴
∴ ,
,
而 又∵
又∵
∴
由于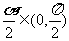 ,∴
,∴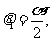 而
而
∴ ∵
∵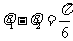 ,∴
,∴
7、解、原式=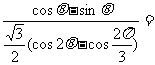
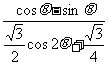
由 ,
,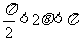 知
知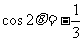 ,
,
∴原式=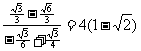
1、C 2、A 3、C 4.D 5. 3或 6.
6.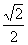
1.A 2.C 3. 4.C 5.B
4.C 5.B
[例题探究]
例1、解:(1)  ,
, ,
, ,又
,又  的最大值
的最大值
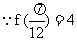 ,
,  ①
, 且
①
, 且
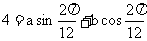 ②,
②,
由 ①、②解出 a=2 , b=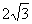 .
.
(2) 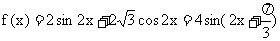 ,
, 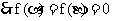 ,
,
 ,
,
 , 或
, 或 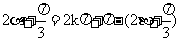 ,
,
即 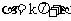 (
(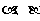 共线,故舍去) , 或
共线,故舍去) , 或  ,
,
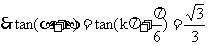
 .
.
[教学建议]:方程组的思想是解题时常用的基本思想方法;在解题时不要忘记三角函数的周期性.
例2、解:(1)∵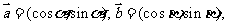 ∴
∴
∵ ∴
∴ ,∴
,∴ .
.
(2)∵ ∴
∴ 而
而 ,∴
,∴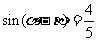
又∵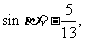 ∴
∴ ∴
∴ .
.
例3、解:设 则
则 ,∴
,∴ ∵
∵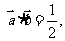
 ∴
∴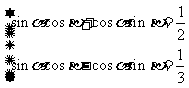 ,∴
,∴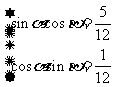 ,
,
∴ ∴
∴ ,
,
∴ .
.
备用题:. 解(1)  ,
, 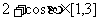 ,
,  ,
,  恒成立.
恒成立.  ,
,  , 即
, 即  恒成立.
恒成立.
 .
.
(2) ,
,  ,
,  ,
, 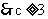 .
.
(3)由题意可知:
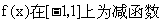 ,
,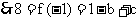 ①,
①,  ② ,由① ,② 可得 b =
② ,由① ,② 可得 b =  ,c = 3 .
,c = 3 .
[教学建议]:赋值法在解决有关恒成立问题时经常用到,利用函数的单调性往往能使问题得以顺利解决。
冲刺强化训练(10)
9.已知向量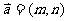 ,
,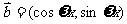 ,其中
,其中 是常数,且
是常数,且 ,
, ,函数
,函数 的周期为
的周期为 ,当
,当 时,函数
时,函数 取得最大值1,
取得最大值1,
(1)求函数 的解析式;
的解析式;
(2)写出 的对称轴方程,并证明.
的对称轴方程,并证明.
第10讲 三角函数的恒等变形与求值
[考前热身]
8.已知向量 ,
,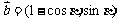 ,
,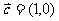 ,
, ,
, 与
与 的夹角为
的夹角为 ,
,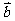 与
与 的夹角为
的夹角为 ,且
,且 -
- =
= ,求
,求 的值
的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com