22．(本题满分14分)

设数列{an}的各项均为正数，前n项和为Sn，已知(n∈N*)．

(1)证明{an}是等差数列，并求an；

(2)设m、k、p∈N*，m+p=2k，求证：+≥；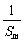

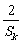(3)对于(2)中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由．

绵阳市高2010级第二次诊断性考试

数学(文)参考解答及评分标准

21．(本题满分12分)

已知椭圆C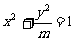：的焦点在y轴上，且离心率为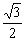．过点(0，3)的直线l与椭圆C相交于两点A、B．

　　 (1)求椭圆C的方程；

(2)若以AB为直径的圆恰好经过椭圆C的右顶点M，求此时l的方程．

20．(本题满分12分)

已知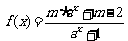(其中a>0且a≠1，m∈R)是定义在R上的奇函数．记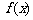的反函数为．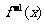

(1)求实数m的值及；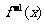

(2)设数列{an}满足an=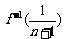(n∈N*)，它的前n项和为Sn，求使不等式Sn<成立的n的取值．

19．(本题满分12分)

已知圆C：x2+y2+2x-4y+1=0．O为坐标原点，动点P在圆C外，过P作圆C的切线，设切点为M．

(1)若点P运动到(1，3)处，求此时切线l的方程；

(2)求满足条件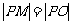的点P的轨迹方程．

18．(本题满分12分)

已知函数f　(x)=mx3+(ax-1)(x-2)(x∈R)的图象在x=1处的切线与直线x+y=0平行．

(1)求m的值；

(2)当a≥0时，解关于x的不等式f　(x)<0．

17．(本题满分12分)

已知向量m=(cosx+sinx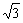，cosx)，n=(cosx-sinx，2sinx)，设函数f　(x) =m · n．

(1)求函数f　(x)的最小正周期T；

(2)若角A是锐角三角形的最大内角，求f　(A)的取值范围．

16．已知数列{an}满足：an = logn+1(n+2)，n∈N*，我们把使a1·a2·…·ak为整数的数k(k∈N*)叫做数列{an}的理想数．给出下列关于数列{an}的几个结论：

① 数列{an}的最小理想数是2；

② {an}的理想数k的形式可以表示为 k = 4n-2(n∈N*)；

③ 在区间(1，1000)内{an}的所有理想数之和为1004；

④ 对任意n∈N*，有an+1>an．

其中正确结论的序号为　　　　　　　　　 　　．

15．在△ABC中，a、b、c是角A、B、C的对边，角A、B、C成等差数列，a=8，b=7，则cosC=　　　　　 ．

14．以椭圆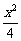+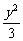=1的右焦点为焦点，以坐标原点为顶点的抛物线方程是　　　　 ．

13．不等式≥0的解集是　　 　　　．(用区间表示)