
2.在力的合成与分解中,下列说法正确的是
A.放在斜面上的物体所受的重力可以分解为沿斜面下滑的力和物体对斜面的压力
B.合力必大于其中一个分力
C.用细绳把物体吊起来,如果说作用力是物体的重力,那反作用力就是物体拉绳的力
D.已知一个力F的大小和方向,则一定可以把它分解为大小都和F相等的两个分力
1.下列说法正确的是
A.物体所受摩擦力的大小不仅跟接触面的性质和物体对接触面的压力有关,有时也跟物体的运动情况有关
B.静摩擦力的方向总是沿接触面的切线方向,且跟物体运动的方向相反
C.滑动摩擦力的大小跟物体对接触面的正压力的大小N成正比,其中N是弹力,在数值上等于物体的重力
D.静摩擦力是变力,压力增大时,静摩擦力也随着增大
22.解:(1)∵  ,
,
∴ 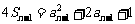 (n≥2).
(n≥2).
两式相减得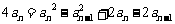 .
.
整理得  ,
,
∵ 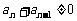 ,
,
∴  (常数).
(常数).
∴ {an}是以2为公差的等差数列.
又 ,即
,即 ,解得
,解得 ,
,
∴ an=1+(n-1)×2=2n-1.………………………………………………………4分
(2)由(1)知 ,∴ Sm=m2,Sp=p2,Sk=k2.
,∴ Sm=m2,Sp=p2,Sk=k2.
 由
由
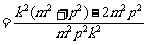
≥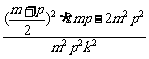 ≥
≥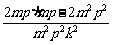 =0,
=0,
即 ≥
≥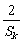 . ………………………………………………………………7分
. ………………………………………………………………7分
(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则 ,
,
∵ 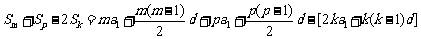
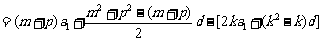 ,
,
把 代入上式化简得
代入上式化简得
 =
=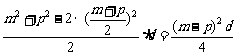 ≥0,
≥0,
∴ Sm+Sp≥2Sk.
又 =
=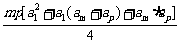
≤
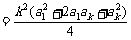

 ,
,
∴ 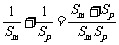 ≥
≥ .
.
故原不等式得证.………………………………………………………………14分
21.解:(1)由题知a2=m,b2=1,∴ c2=m-1.
∴ 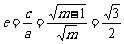 ,解得m=4.
,解得m=4.
∴ 椭圆的方程为 . …………………………………………………4分
. …………………………………………………4分
(2)由(1)知M(1,0),且据题知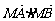 =0.
=0.
当l的斜率不存在时,A(0,2),B(0,-2),
∴  =(-1,2),
=(-1,2), =(-1,-2),
=(-1,-2),
∴ 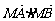 =(-1)×(-1)+2×(-2)=-3≠0,不符合条件.……………………6分
=(-1)×(-1)+2×(-2)=-3≠0,不符合条件.……………………6分
当l的斜率存在时,设l的斜率为k,则l的方程为y=kx+3.
设A(x1,y1),B(x2,y2),于是 =(x1-1,y1),
=(x1-1,y1), =(x2-1,y2).
=(x2-1,y2).
联立l和椭圆的方程: 消去y,整理得(4+k2)x2+6kx+5=0,
消去y,整理得(4+k2)x2+6kx+5=0,
∴ Δ=(6k)2-4×(4+k2)×5=16k2-80>0,解得k2>5.
且 ,
,
∴
y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9= . …………………10分
. …………………10分
∵ 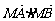 =x1x2-(x1+x2)+1+y1y2
=x1x2-(x1+x2)+1+y1y2
=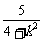 +
+ +1+
+1+
= ,
,
∴  =0,解得k=-3,或k=5(均满足条件).
=0,解得k=-3,或k=5(均满足条件).
∴ l的方程为y=-3x+3,或y=5x+3.………………………………………12分
20.解:(1)f (x)是定义在R上的奇函数,
∴ f (0)=0,即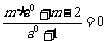 ,解得m=1. ………………………………2分
,解得m=1. ………………………………2分
∴  (x∈R).
(x∈R).
令 ,反解得
,反解得 ,
,
∴  (-1<x<1). ……………………………………………6分
(-1<x<1). ……………………………………………6分
(2)由已知有an=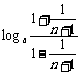 =
= (n∈N*),
(n∈N*),
∴ Sn= +
+ +
+ +…+
+…+
=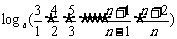
=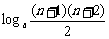 . ………………………………………………………9分
. ………………………………………………………9分
于是由题得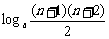 <
< ,
,
∴ 当a>1时, <6,解得-5<n<2.
<6,解得-5<n<2.
 当0<a<1时,
当0<a<1时, >6,解得n<-5,或n>2.
>6,解得n<-5,或n>2.
∵ n∈N*,
∴ 当a>1时,n=1;当0<a<1时,n取大于2的所有整数. …………12分
19.解:把圆C的方程化为标准方程为(x+1)2+(y-2)2=4,
∴ 圆心为(-1,2),半径为2. ………………………………………………2分
(1)当l的斜率不存在时,此时l的方程为x=1,满足条件.……………4分
当l的斜率存在时,设斜率为k,得l的方程为y-3=k(x-1),即kx-y+3-k=0,
∵ 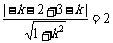 ,解得
,解得  .
.
∴ l的方程为3x+4y-15=0.
综上,满足条件的切线l的方程为x=1或3x+4y-15=0. …………………7分
(2)设P(x,y),
∵ |PM|2=|PC|2-|MC|2=(x+1)2+(y-2)2-4,|PO|2=x2+y2,
∴ 由|PM|=|PO|有(x+1)2+(y-2)2-4=x2+y2,
整理得2x-4y+1=0,
即点P的轨迹方程为2x-4y+1=0. …………………………………………12分
18.解:(1)∵ f (x)=mx3+ax2-(2a+1)x+2,
∴ .
.
∴ ,
,
即函数f (x)的图象在x=1处的切线斜率为3m-1.
∴由题知3m-1=-1,解得m=0.
(2)由(1)知f (x)=(ax-1)(x-2).
当a=0时,f (x)=-(x-2)>0,解得x<2.
当a>0时,方程f (x)=0的两根为 ,x2=2
,x2=2
若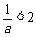 即
即 时,原不等式的解为
时,原不等式的解为 ;
;
若 即
即 时,原不等式的解为Æ;
时,原不等式的解为Æ;
若 即
即 时,原不等式的解为
时,原不等式的解为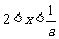 .
.
∴综上所述,当a=0时,原不等式的解集为{x|x<2};
 当0<a<
当0<a<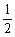 时,原不等式的解集为{x|
时,原不等式的解集为{x| };
};
当 时,原不等式的高@考@资@源@网解集为Æ;
时,原不等式的高@考@资@源@网解集为Æ;
当 时,原不等式的解集为{x|
时,原不等式的解集为{x|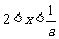 }.………………………12分
}.………………………12分
17.解:(1)由已知有f
(x)=(cosx+sinx)(cosx-sinx)+ ·2sinx
·2sinx

 ,………………………………………6分
,………………………………………6分
于是T ,即f(x)的最小正周期为π. ………………………………8分
,即f(x)的最小正周期为π. ………………………………8分
(2)由已知有 A∈ ,
,
∴  ≤
≤ .
.
∴ -1< ≤1.
≤1.
即f (A)的取值范围是 .………………………………………………12分
.………………………………………………12分
13. 14.y2=4x 15.
14.y2=4x 15.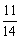 或
或 16.①③
16.①③
CBBCD AABDC CB
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com