22．(本小题满分15分)

已知函数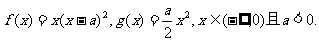

　 (I)(i)求函数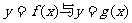的图象的交点A的坐标；

　　　　 (ii)设函数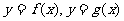的图象在交点A处的切线分别为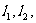是否存在这样的实数a，使得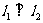？若存在，请求出a的值和相应的点A坐标；若不存在，请说明理由。

　 (II)记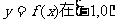上最小值为F(a)，求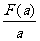的最小值。

21．(本小题满分15分)

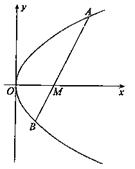
已知抛物线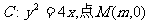在x轴的正半轴上，过M的直线与C相交于A、B两点，O为坐标原点。

　 (I)若m=1，且直线的斜率为1，求以AB为直径的圆的方程；

　 　 (II)问是否存在定点M，不论直线绕点M如何转动，使得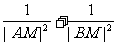恒为定值。

20．(本小题满分14分)

　　　　 如图所示，在直角梯形ABCP中，AB=BC=3，AP=7，CD⊥AP，现将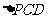沿折线CD折成60°的二面角P-CD-A，设E，F，G分别是PD，PC，BC的中点。

　 (I)求证：PA//平面EFG；

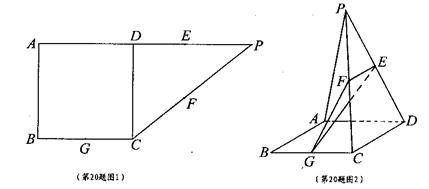　 　 (II)若M为线段CD上的一个动点，问当M在什么位置时，MF与平面EFG所成角最大。

19．(本小题满分14分)

某人随机地将编号为1，2，3，4的四个小球放入编号为1，2，3，4的四个盒子中，每个盒子放一个小球，全部放完。

　 (I)求编号为奇数的小球放入到编号为奇数的盒子中的概率值；

　 (II)当一个小球放到其中一个盒子时， 若球的编号与盒子的编号相同 ，称这球是“放对”的，否则称这球是“放错”的。设“放对”的球的个数为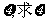的分布列及数学期望。

18．(本小题满分14分)

　　 已知函数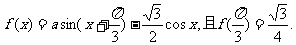

　 (I)求实数a的值；

　 (II)求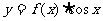的最小正周期和单调增区间。

17．已知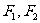分别是椭圆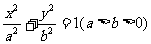的左、右焦点，上顶点为M。若在椭圆上存在一点P，分别连结PF₁，PF₂交y轴于A，B两点，且满足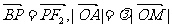，则实数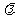的取值范围为　　　　　　　 。

16．在杨辉三角中，如图的每条斜线上的数字之和构

成数列 ，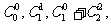

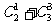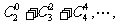
则这个数列的第9项的表达式为　　　　　 。

14．某地四所学校组织学生到当地的爱国主义教育基地参加社会实践活动。该基地每天 只能安排一所学校，其中A学校因人数较多，要连续安排2天，其余的三所学校各安排1天，则该基地连续7天中不同的安排方法的种数共有　　 。(用数字作答)

　 15．已知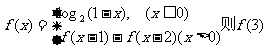的值等于　　　　　 。

13．已知实数x，y满足约束条件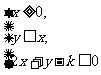时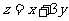，的最大为12，则实数k的值等于　　　 。

12．用分层抽样的方法从某学校的高中学生中抽取一个容量为45的样本，其中高一年级抽20人， 高三年级抽10人。已知该校高二年级共有300人，则该校高中学生总人数为

　　 　　　　　　人。