
31.(奉贤)(12分)如图所示,在动摩擦因素μ=0.2的水平面AB上,水平恒力F推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点。用传感器测量物体的瞬时速度,并在表格中记录了部分测量数据。求:
|
t/s |
0.0 |
0.2 |
0.4 |
… |
2.2 |
2.4 |
2.6 |
… |
|
v/m•s-1 |
0.0 |
0.4 |
0.8 |
… |
3.0 |
2.0 |
1.0 |
… |
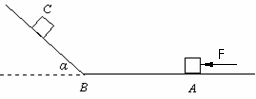 (1)恒力F 的大小;
(1)恒力F 的大小;
(2)斜面的倾角 ;
;
(3)若在A处撤去推力F,给物体一个水平向左的初速度 ,恰能使物体运动到C点,求此初速度
,恰能使物体运动到C点,求此初速度 的大小。
的大小。
(1)物体从 A 到 B 过程中: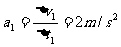 (1分
(1分 )
)
∴ F=ma1+mmg=4N (2分)
(2)物体从 B 到 C 过程中: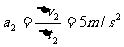 (1分)
(1分)
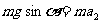 ∴
∴ 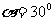 (2分)
(2分)
(3)当物体在推力F的作用下在AB间运动时,设AB间的距离为S,通过AB时间的t,
通过B点时的速度为vB,根据表中提供的数据,在0-2.6s时间段内:
当物体在水平面上运动时 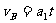
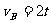
当物体在斜面上运动时 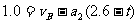
 (1分)
(1分)
解得 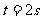
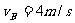 (1分)
(1分)
又 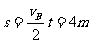 (1分)
(1分)
给物体一个初速度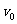 时物体恰能运动到C点,由于斜面光滑,则物体通过B点的速
时物体恰能运动到C点,由于斜面光滑,则物体通过B点的速
度仍为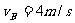 ,根据动能定理:
,根据动能定理: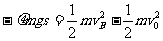 (2分)
(2分)
解得 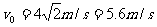 (1分)
(1分)
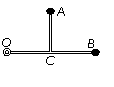 (闸北)31.(12分)如图所示,一根“┻”形状的轻支架上固定两个小球A、B,支架可以绕转轴O在竖直平面内无摩擦自由转动,已知mA=2kg,mB=1kg,AC=BC=OC=1m。(g取10m/s2)。
(闸北)31.(12分)如图所示,一根“┻”形状的轻支架上固定两个小球A、B,支架可以绕转轴O在竖直平面内无摩擦自由转动,已知mA=2kg,mB=1kg,AC=BC=OC=1m。(g取10m/s2)。
(1)在A球上施加一个力F,使装置静止,B与转轴O在同一水平线上。则F最小为多少?
(2)撤去F,当A球摆动到最低点时,B球速度多大?
解:(1)力F最小,则F应与OA连线垂直 (1分)
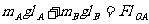 (2分)
(2分)
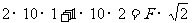 (1分)
(1分)
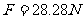 (1分)
(1分)
(2)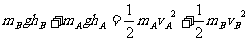 (2分)
(2分)
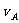 :
: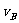 =
=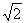 :2
(1分)
:2
(1分)
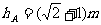 (1分)
(1分)
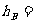
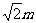 (1分)
(1分)
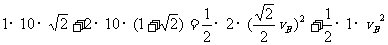 (1分)
(1分)
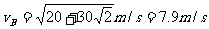 (1分)
(1分)
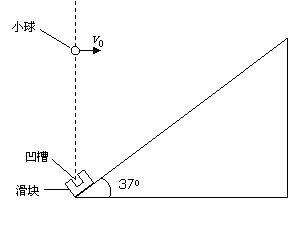 (闸北)32.(14分)如图所示,倾角为37°的粗糙斜面的底端有一质量
(闸北)32.(14分)如图所示,倾角为37°的粗糙斜面的底端有一质量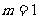 kg的凹形小滑块,小滑块与斜面间的动摩擦因数
kg的凹形小滑块,小滑块与斜面间的动摩擦因数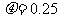 。现小滑块以某一初速度
。现小滑块以某一初速度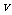 从斜面底端上滑,同时在斜面底端正上方有一小球以
从斜面底端上滑,同时在斜面底端正上方有一小球以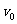 水平抛出,经过0.4s,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中。(已知
水平抛出,经过0.4s,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中。(已知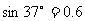 ,
,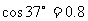 ),g取10m/s2,求:
),g取10m/s2,求:
(1)小球水平抛出的速度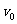 。
。
(2)小滑块的初速度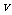 。
。
(3)0.4s内小滑块损失的机械能 。
。
解:(1)设小球落入凹槽时竖直速度为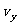
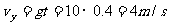 (2分)
(2分)
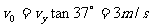 (2分)
(2分)
(2)小球落入凹槽时的水平位移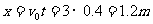 (2分)
(2分)
则滑块的位移为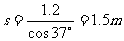 (1分)
(1分)
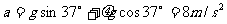 (2分)
(2分)
根据公式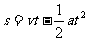 (1分)
(1分)
得: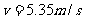 (1分)
(1分)
(3)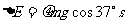 (2分)
(2分)
 (1分)
(1分)


全 品中考网
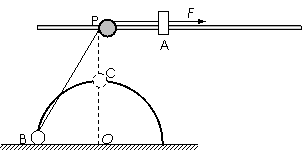
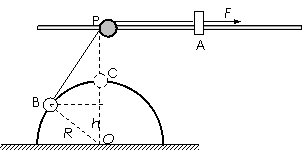
33.(宝山)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A。半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响。现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(1)求把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功。
(2)求小球B运动到C处时所受的向心力的大小。
(3)问小球B被拉到离地多高时滑块A与小球B的速度大小相等?
(1)对于F的做功过程,有
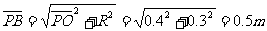 , (1分){33.1}
, (1分){33.1}
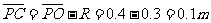 (1分){33.2}
(1分){33.2}
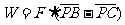 (1分){33.3}
(1分){33.3}
所以,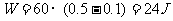 (1分){33.4}
(1分){33.4}
(2)由于B球到达C处时,已无沿绳的分速度,所以此时滑块A的速度为零,
考察两球及绳子组成的系统的能量变化过程,由功能关系,得
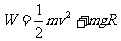 , (2分){33.5}
, (2分){33.5}
代入已知量,得
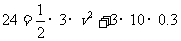 (1分){33.6}
(1分){33.6}
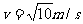 (1分){33.7}
(1分){33.7}
因为向心力公式为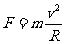 (1分){33.8}
(1分){33.8}
所以,代入已知量,得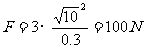 (1分){33.9}
(1分){33.9}
(3)当绳与轨道相切时两球速度相等,
由相似三角形知识,得
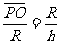 (2分){33.10}
(2分){33.10}
代入已知量,得
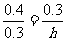 (1分){33.11}
(1分){33.11}
所以,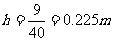 (1分){33.12}
(1分){33.12}
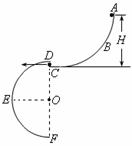
(普陀) 29、(12分)如图所示,ABC和DEF是在同一竖直平面内 的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合。现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放,
的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合。现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放,
(1)若要使小球经C处水平进入轨道DEF且能沿轨道运动,H至少要有多高?
(2)若小球静止释放处离C点的高度h小于(1)中H的最小值,小球可击中与圆心等高的E点,求此h的值。(取g=10m/s2)
解:(1)小球从ABC轨道下滑,机械能守恒,设到达C点时的速度大小为v。则:
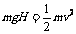 2分
2分
小球 能在竖直平面内做圆周运动,在圆周最高点必须满足:
能在竖直平面内做圆周运动,在圆周最高点必须满足:
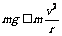 2分
2分
联立以上两式并代入数据得: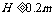 2分
2分
(2)若h<H,小球过C点后做平抛运动,设球经C点时的速度大小为vx,则击中E点时:竖直方向: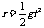 1分
1分
水平方向: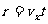 1分
1分
由机械能守恒有: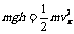 2分
2分
联立以上三式并代入数据得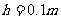 2分
2分
31.(徐汇)(12分)在研究摩擦力特点的实验中,将木块放在水平长木板上,如图(a)所示,用力沿水平方向拉木块,拉力从零开始逐渐增大。分别用力传感器采集拉力和木块所受到的摩擦力,并用计算机绘制出摩擦力Ff 随拉力F的变化图像,如图(b)所示。已知木块质量为0.78kg,重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80。
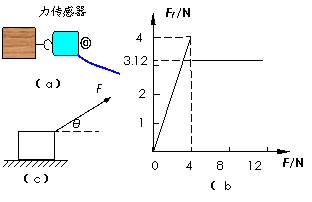 (1)求木块与长木板间的动摩擦因数;
(1)求木块与长木板间的动摩擦因数;
(2)如图(c),若木块在与水平方向成37°角斜向右上方的恒定拉力F作用下,以a=2m/s2的加速度从静止开始沿水平面做匀变速直线运动,拉力大小应为多大?
(3)在(2)中力作用2s后撤去拉力F,再经过多少时间木块停下?整个运动过程中摩擦力对木块做了多少功?
(1)由(b)图可知,木块所受到的滑动摩擦力Ff=3.12N (1分)
由Ff=μFN (1分) 得 μ===0.4 (1分)
(2)根据牛顿运动定律得:Fcosθ-Ff=ma(1分)Fsinθ+FN=mg (1分) Ff=μFN
联立各式得:F=4.5N (2分)
(3)撤去拉力后a′=μg=4m/s2(1分),所以停下的时间t2==1s(1分)
应用动能定理得:Fs1cosθ+Wf=0(1分)
s1=at12=4m(1分) 代入数据得Wf =-14.4J (1分)
(杨浦) 30.(10分)如图所示是录自明代《天工开物》中的一幅图,它描述
30.(10分)如图所示是录自明代《天工开物》中的一幅图,它描述 的是我同古代的一种农业机械,叫做水碾.它是利用水的动能来做功的装置.当水冲击下部水轮时,转动的轮子会带动上部的石碾来碾米.水从右边进入,左边流出.假若每秒钟冲击叶片的水流为10 kg,水速从5 m/s减小为1 m/s.则每秒钟水流对叶轮做的功为多大?
的是我同古代的一种农业机械,叫做水碾.它是利用水的动能来做功的装置.当水冲击下部水轮时,转动的轮子会带动上部的石碾来碾米.水从右边进入,左边流出.假若每秒钟冲击叶片的水流为10 kg,水速从5 m/s减小为1 m/s.则每秒钟水流对叶轮做的功为多大?
解:每秒钟水流的动能变化为:
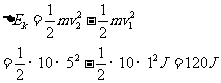 (得6分)
(得6分)
水流对叶轮做功等于水流的动能变化:
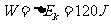 (得3分)
(得3分)
答:每秒钟水流对叶轮做的功为120J。(得1分)
(闵行) 32.(13分)如图所示,在竖直平面内有一个半径为R且光滑的四分之一圆弧轨道AB,轨道下端B与水平面BCD相切,BC部分光滑且长度大于R,C点右边粗糙程度均匀且足够长。现用手捏住一根长也为R、质量为m的柔软匀质细绳的上端,使绳子的下端与A点等高,然后由静止释放绳子,让绳子沿轨道下滑。重力加速度为g。求:
(1)绳子前端到达C点时的速度大小;
 (2)若绳子前端在过C点后,滑行s距离后停下,而且s>R,试计算绳子与粗糙平面间的动摩擦因数。
(2)若绳子前端在过C点后,滑行s距离后停下,而且s>R,试计算绳子与粗糙平面间的动摩擦因数。
(1)绳子由释放到前段达C点过程中,由机械能守恒定律得:
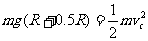 (5分)
(5分)
解得: (1分)
(1分)
(2)绳子前端滑过C点后,其受到的摩擦力先均匀增大,其平均值为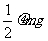 ,前端滑行R后摩擦力不变,其值为
μmg (2分)
,前端滑行R后摩擦力不变,其值为
μmg (2分)
由动能定理得:
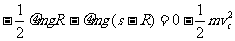 (3分)
(3分)
把 代入上式解得:
代入上式解得: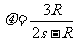 (2分)
(2分)
(青浦) 32、(12分)如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经过B点后进入粗糙水平面(经过B点时速度大小不变而方向变为水平)。已知SAB=3m,SBC=7.6m ,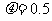 。试求:
。试求:
(1)若在小物体上始终施加一个水平向左的恒力F,发现当F=F0时,小物体恰能从A点静止出发,沿ABC到达水平面上的C点停止。求F0的大小。
(2)某同学根据(1)问的结果,得到如下判断:“当F≥F0时,小物体一定能从A点静止出发,沿ABC到达C点。”这一观点是否有疏漏,若有,请对F的范围予以补充。(sin37°=0.6,cos37°=0.8)
(1)对A到C列动能定理:
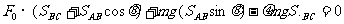 (4分)
(4分)
F0=2N
 (2分)
(2分)
(本小题也可以分段列式,或用牛顿定律求解,请老师自己决定评分标准)
(2)有疏漏,F太大物体会离开斜面,而不能沿ABC运动。 (2分)
临界状态为物体沿斜面运动但与斜面没有弹力,此时
F=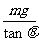 =13.3N (2分) 得13.3N≥F≥2N (2分)
=13.3N (2分) 得13.3N≥F≥2N (2分)
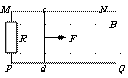
(青浦) 33、(16分)如图所示,MN、PQ为水平放置的足够长的平行光滑导电导轨,间距L为0.5m,导轨左端连接一个2Ω的电阻R,将一根质量为0.2kg的金属棒cd垂直地放在导轨上,且与导轨接触良好,金属棒的电阻r大小为1Ω,导轨的电阻不计,整个装置放在磁感应强度为1T的匀强磁场中,磁场方向垂直于导轨平面向下,现对金属棒施加一水平向右的拉力F,使棒从静止开始向右运动。当棒的速度达到3m/s后保持拉力的功率恒为3W,从此时开始计时,即此时t=0,已知从此时直至金属棒达到稳定速度的过程中电流通过电阻R做的功为2.2J。试解答以下问题:
(1)金属棒达到的稳定速度是多少?
(2)金属棒从t=0开始直至达到稳定速度所需的时间是多少?
(3)试估算金属棒从t=0开始直至达到稳定速度的过程中通过
电阻R的电量大约在什么数值范围内?
(1)匀速: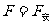 (1分)
(1分)
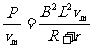 (2分)
(2分) 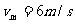 (1分)
(1分)
(2)根据动能定理:
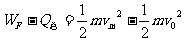 (2分)
(2分)
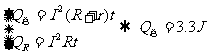 (2分)
(2分) 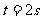 (1分)
(1分)
 (3)
(3)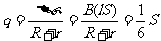 (2分)
(2分)
根据画出的 图象得:
(1分)
图象得:
(1分)
 (1分)
(1分)
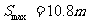 (1分)
(1分)
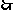
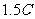 <
<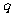 <
<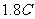 (2分)
(2分)
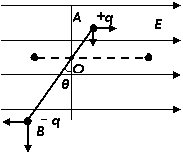
(浦东) 32.(14分)如图所示,绝缘轻杆长L=0.9m,两端分别固定着带等量异种电荷的小球A、B,质量分别为mA=4×10-2kg,mB=8×10-2kg,A球带正电,B球 带负电,电荷量q=6.0×10-6C。轻杆可绕过O点的光滑水平轴转动,OB=2OA。一根竖直细线系于杆上OB中点D使杆保持水平,整个装置处在水平向右的匀强电场中,电场强度E=5×104N/C。不计一切阻力,取g=10m/s2,求:
带负电,电荷量q=6.0×10-6C。轻杆可绕过O点的光滑水平轴转动,OB=2OA。一根竖直细线系于杆上OB中点D使杆保持水平,整个装置处在水平向右的匀强电场中,电场强度E=5×104N/C。不计一切阻力,取g=10m/s2,求:
(1)细线对杆的拉力大小;
(2)若将细线烧断,当轻杆转过90°时,A、B两小球电势能总的变化量;
 (3)细线烧断后,在杆转动过程中小球A的最大速度。
(3)细线烧断后,在杆转动过程中小球A的最大速度。
(1)根据有固定转动轴物体的平衡条件,有
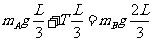 (2分)
(2分)
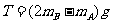 =(2×8×10-2-4×10-2)×10=1.
=(2×8×10-2-4×10-2)×10=1. 2(N) (2分)
2(N) (2分)
(2)杆转过90°时,电场力对两带电小球做正功,电势能减少 (1分)
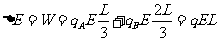 =6.0×10-6×5×104×0.9=0.27(J)(3分)
=6.0×10-6×5×104×0.9=0.27(J)(3分)
(3)当力矩的代数和为零时,B球的速度达到最大。
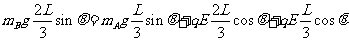
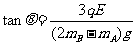 =
=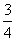
θ=37° (2分)
由动能定理

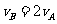 (以上二式共2分)
(以上二式共2分)
联立求得:vA=2m/s (2分)
(卢湾) 31、冰壶比赛是在水平冰面上进行的体育项目,比赛场地示意如图所示。比赛时,运动员在投掷线AB处让冰壶以一定的初速度滑出,使冰壶的停止位置尽量靠近距离投掷线30m远的O点。为使冰壶滑行得更远,运动员可以用毛刷擦冰壶运行前方的冰面,使冰壶与冰面间的动摩擦因数减小。设冰壶与冰面间的动摩擦因数为μ1=0.008,用毛刷擦冰面后动摩擦因数减少至μ2=0.004。在某次比赛中,运动员使冰壶C在投掷线中点处以v0=2m/s的速度沿虚线滑出。
(1)若不用毛刷擦冰面,则冰壶停止的位置距离O点多远?
(2)为使冰壶C能够沿虚线恰好到达O点,运动员用毛刷擦冰面的长度应为多少?
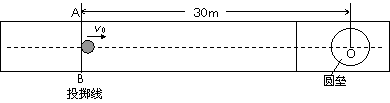
(1)mv02=μ1mgs(2分) s= =m = 25m(2分)
30m-25m=5m(1分)
(2)设冰壶在未被毛刷擦过的冰面上滑行的距离为s1,所受摩擦力的大小为f1:在被毛刷擦过的冰面上滑行的距离为s2,所受摩擦力的大小为f2。则有
s1+ s2=L ①(式中L为投掷线到圆心O的距离)
f1=μ1mg ② ,f2=μ2mg③ 由功能关系,得f1 s1+ f2 s2=mv02 ④(4分)
联立以上各式,解得s2= 代入数据得 s2=10m(2分)
(黄浦) 32.(13分)如图23-1所示,长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处连接,有一质量为2kg的滑块,从A处由静止开始受水平向右的力F作用,F按图23-2所示规律变化,滑块与AB和BC间的动摩擦因数均为0.25,重力加速度g取10m/s2。求:
32.(13分)如图23-1所示,长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处连接,有一质量为2kg的滑块,从A处由静止开始受水平向右的力F作用,F按图23-2所示规律变化,滑块与AB和BC间的动摩擦因数均为0.25,重力加速度g取10m/s2。求:
(1)滑块到达B处时的速度大小;
 (2)不计滑块在B处的速率变化,滑块冲上斜面,滑块最终静止的位置与B点的距离。
(2)不计滑块在B处的速率变化,滑块冲上斜面,滑块最终静止的位置与B点的距离。
(1)由图得:0~2m:
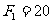 N △X1=2m;
(1分)
N △X1=2m;
(1分)
2~3m: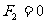 ,△X2=1m;
(1分)
,△X2=1m;
(1分)
3~4m: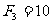 N,△X3=1m
(1分)
N,△X3=1m
(1分)
A至B由动能定理: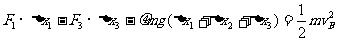 (2分)
(2分)
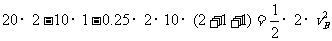 得
得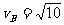 m/s
(1分)
m/s
(1分)
(2)因为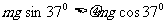 ,滑块将滑回水平面。
(1分)
,滑块将滑回水平面。
(1分)
设滑块由B点上滑的最大距离为L,
由动能定理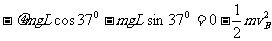 (2分)
(2分)
解得: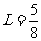 m
(1分)
m
(1分)
从最高点滑回水平面,设停止在与B点相距S处,
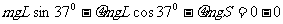 (1分)
(1分)
解得: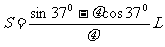 (1分)
(1分)
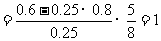 m
m
 (1分)
(1分)
(虹口) 31、(12分)弹性小球从某一高度H自由下落到水平地面上,与水平地面碰撞后弹起,假设小球与地面的碰撞过程中没有能量损失,但由于受到大小不变的空气阻力的影响,使每次碰撞后弹起上升的高度是碰撞前下落高度的3/4。为使小球弹起后能上升到原来的高度H,则需在小球开始下落时,在极短时间内给它一个多大的初速度v0?
某同学对此解法是:由于只能上升H,所以机械能的损失为mgH,只要
补偿损失的机械能即可回到原来的高度,因此mv02=mgH,得v0 =
你同意上述解法吗?若不同意,请简述理由并求出你认为正确的结果。
解:不同意,该学生只考虑小球回到H后要继续上升所需克服重力做功的动能,忽略了继续上升时还要有能量克服空气阻力做功。
 (4分)
(4分)
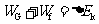
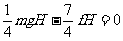
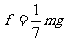 (4分)
(4分)
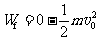
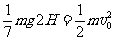
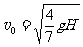 (4分)
(4分)
(虹口) 33、(15分)风洞实验室可产生水平方向的、大小可调节的风力。在风洞中有一个固定的支撑架ABC,该支撑架的外表面光滑,且有一半径为R的四分之一圆柱面,支撑架固定在离地面高为2R的平台上,平台竖直侧壁光滑,如图所示,地面上的D点处有一竖直的小洞,小洞离侧壁的水平距离为R,现将质量分别为m1和m2的两个小球用一根不可伸长的轻绳连接按图示的方式置于圆柱面上,球m1放在柱面底部的A点,球m2竖直下垂。
(1)在无风情况下,将两球由静止释放(不计一切摩擦),小球m1沿圆柱面向上滑行,到最高点C恰与圆柱面脱离,则两球的质量之比m1: m2是多少?(m1到最高点时m2尚未着地)
(2)改变两小球的质量比,并使它们由静止开始运动,同时开动风机,产生均匀、恒定、水平向左的风,当小球m1滑至圆柱面的最高点C时绳恰好断裂,通过调节风力F的大小,使小球m1恰能与洞壁无接触地落入小洞D的底部,求小球m1经过C点时的速度及水平风力F的大小。
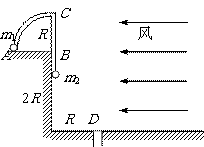
解:(1)小球m1在C点恰好离开圆柱面,由圆周运动规律可知小球在C点时只由重力提供向心力,
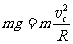 ,速度为:
,速度为: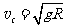 1 (3分)
1 (3分)
由m1和m2组成的系统机械能守恒,则将两球由静止释放到小球m1离开C点时有:
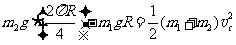 2 (2分)
2 (2分)
由12式解得: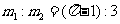 (1分)
(1分)
(2)绳子断裂后小球m1在水平方向的平均速度为: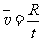 3 (1分)
3 (1分)
小球m1在下落过程中在竖直方向做自由落体运动,运动时间为: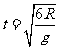 4 (2分)
4 (2分)
小球m1在水平方向做末速度为零的匀减速运动,小球m1在离开C点时的速度为:
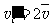 5 (1分)
5 (1分)
由12345解得: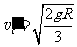 (2分)
(2分)
由匀变速运动规律可知,小球在水平方向的加速度大小为:
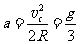 6 (2分)
6 (2分)
由牛顿第二定律可求得小球所受风力为:  (1分)
(1分)
2.72m;0.384J
 (嘉定)32、(12分)如图所示,半径r=0.3m、质量M的光滑1/4圆弧面放在光滑的水平长桌面上,桌面离地面高h=0.8m。将一质量为m小物体从圆弧最高处静止释放,为了防止圆弧面在桌面上的滑动,在圆弧面右侧固定了档板。若两物体的质量满足M=2m。求
(嘉定)32、(12分)如图所示,半径r=0.3m、质量M的光滑1/4圆弧面放在光滑的水平长桌面上,桌面离地面高h=0.8m。将一质量为m小物体从圆弧最高处静止释放,为了防止圆弧面在桌面上的滑动,在圆弧面右侧固定了档板。若两物体的质量满足M=2m。求
(1)小物体由静止释放后,小物体的水平射程x。
(2)某次操作中忘记安装档板,发现小物体静止释放后,圆弧面开始向右运动,最后测得小物体的水平射程x0=0.8m,则小物体滑离后圆弧面在桌面上运动的最大速度vM。
解:(1)(6分)设小物体到达圆弧底端速度v,则下滑的过程中由动能定理得
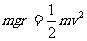 ……①(或用机械能守恒定律) (2分)
……①(或用机械能守恒定律) (2分)
小物体做平抛运动有
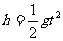 ……②
……②  ……③ (2分)
……③ (2分)
由上述列式得x≈0.98m (2分)
(2)(6分)小物体离开圆弧面后,圆弧面速度最大
设小物体离开桌面速度v1,圆弧面速度v2。
小物体做平抛运动有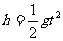
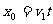 (2分)
(2分)
小球下滑中和圆弧面整体用动能定理
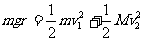 (2分)
得v2=1 m/s。 (2分)
(2分)
得v2=1 m/s。 (2分)
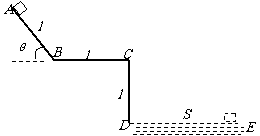 (长宁)30.(10分)如图所示的ABC是游乐场中的滑道模型,它位于竖直平面内,BC滑道水平,A B与水平面夹角为θ,DE是水面,AB = BC = CD =
(长宁)30.(10分)如图所示的ABC是游乐场中的滑道模型,它位于竖直平面内,BC滑道水平,A B与水平面夹角为θ,DE是水面,AB = BC = CD =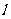 .滑船(可视为小滑块)从A点由静止开始下滑,滑船与AB滑道间的动摩擦因数为μ,滑船落水点到竖直岸的水平距离为S,不计空气阻力,试求:
.滑船(可视为小滑块)从A点由静止开始下滑,滑船与AB滑道间的动摩擦因数为μ,滑船落水点到竖直岸的水平距离为S,不计空气阻力,试求:
(1)滑船滑至C点时的速度;
(2)滑船滑至B 点时的速度.
(1)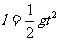
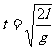 得
得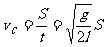 (4分)
(4分)
(2) 可以用动能定理求,也可以用运动学公式联系牛顿第二定律求得:
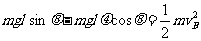 (4分)
(4分)
求得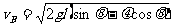 (2分)
(2分)
0.45,2
 (闸北)23.将一质量为0.2kg的小球在空中静止释放,其离地高度与时间的关系
(闸北)23.将一质量为0.2kg的小球在空中静止释放,其离地高度与时间的关系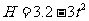 ,式中
,式中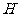 以m为单位,
以m为单位,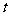 以s为单位。则小球0.4
以s为单位。则小球0.4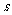 末离地高度为 m,克服空气阻力所做的功为
J。(g取10m/s2)
末离地高度为 m,克服空气阻力所做的功为
J。(g取10m/s2)
25.(徐汇)如图所示,半径R=0.6m的光滑半圆细环竖直放置并固定在水平桌面上,环上套有质量为1kg的小球甲,用一根细线将小球甲通过两个光滑定滑轮B、D与质量为2kg的小物体乙相连,滑轮的大小不计,与半圆环在同一竖直平面内,它们距离桌面的高度均为h=0.8m,滑轮B恰好在圆环最高点C点的正上方。初始时将甲拉至半圆环左边最低点A处,然后将甲、乙由静止开始释放,则当甲运动到离桌面高度为_________m时,甲、乙速度大小相等;当甲运动到C点时的速度大小为________m/s。(g=10m/s2)
25.(长宁)某物块以80 J初动能从固定斜面底端上滑,以斜面底端为零势能参考平面,到达最高点时物块的重力势能为50 J.在返回斜面底端的过程中,当物块的重力势能为20 J时,动能为_______J;当物块下滑到动能和势能恰好相等时,其机械能为___________J .
12J 200/7 J (28.6 J)
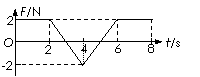
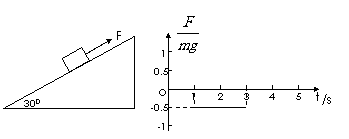 (嘉定)25.如图所示,在倾角为300的足够长的光滑斜面上有一质量为m=1kg的物体,它受到沿斜面方向的力F的作用。力F按右图变化(图中纵坐标是力F与mg的比值,力F沿斜面向上为正)。已知此物体在t=0时速度为零,那么此物体在4s末的速率为 ________ m/s,力F做的功是 ________ J。(g取10m/s2)
(嘉定)25.如图所示,在倾角为300的足够长的光滑斜面上有一质量为m=1kg的物体,它受到沿斜面方向的力F的作用。力F按右图变化(图中纵坐标是力F与mg的比值,力F沿斜面向上为正)。已知此物体在t=0时速度为零,那么此物体在4s末的速率为 ________ m/s,力F做的功是 ________ J。(g取10m/s2)
30 m/s;150J
 (卢湾)24、特种兵过山谷的一种方法可化简为如右图所示的模型:将一根长为2d、不可伸长的细绳的两端固定在相距为d的A、B两等高处,悬绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP竖直,则此时甲对滑轮的水平拉力为_________;若甲将滑轮由静止释放,则乙在滑动中速度的最大值为_________。(不计滑轮与绳的质量,不计滑轮的大小及摩擦)
(卢湾)24、特种兵过山谷的一种方法可化简为如右图所示的模型:将一根长为2d、不可伸长的细绳的两端固定在相距为d的A、B两等高处,悬绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP竖直,则此时甲对滑轮的水平拉力为_________;若甲将滑轮由静止释放,则乙在滑动中速度的最大值为_________。(不计滑轮与绳的质量,不计滑轮的大小及摩擦)
1/2mg,
(宝山)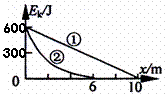 25.有一种利用蓄电池提供动力的电动自行车装有发电机,当关闭动力让车滑行时,发电机利用充电装置可向车载的蓄电池充电,则充电过程是将________能转化成化学能的过程。现有某人骑这样的电动车自行车,以600J的初动能在粗糙的水平路面上滑行,第一次关闭发电机充电装置,让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动发电机充电装置,其动能随位移变化的关系如图线②所示,设前后二次地面和空气对车产生的阻力恒定且相等,则第二次时蓄电池增加的化学能最多是_________ J。
25.有一种利用蓄电池提供动力的电动自行车装有发电机,当关闭动力让车滑行时,发电机利用充电装置可向车载的蓄电池充电,则充电过程是将________能转化成化学能的过程。现有某人骑这样的电动车自行车,以600J的初动能在粗糙的水平路面上滑行,第一次关闭发电机充电装置,让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动发电机充电装置,其动能随位移变化的关系如图线②所示,设前后二次地面和空气对车产生的阻力恒定且相等,则第二次时蓄电池增加的化学能最多是_________ J。
电;240
(奉贤) 24.如图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长,物块A由静止从图示位置释放后,先沿杆向上运动。设某时刻物块A向上运动的速度大小为vA,轻绳与杆的夹角为θ,则此时小球B运动的速度大小vB为__________。在A上升过程中小球B的机械能的变化情况是_________。(填“一直减小”“一直变大”“一直不变”“先变小后变大”或“先变大后变小”)
24.如图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长,物块A由静止从图示位置释放后,先沿杆向上运动。设某时刻物块A向上运动的速度大小为vA,轻绳与杆的夹角为θ,则此时小球B运动的速度大小vB为__________。在A上升过程中小球B的机械能的变化情况是_________。(填“一直减小”“一直变大”“一直不变”“先变小后变大”或“先变大后变小”)
_vA cosθ__ 先变小后变大
(浦东)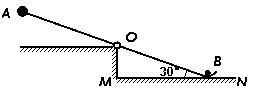 23.如图是一种抛物器,轻质杠杆左端A是一个质量为M=10kg的重球,杠杆的右端是一个被抛的物体,质量为m=0.5kg,OA=OB=1m。此时杠杆与水平地面MN的夹角为θ=30°,要使其静止,则杆右端B应施加一个竖直向下的力F=________N;撤去F,杠杆逆时针转动,物体最后被竖直向上抛出,则物体上升离地面MN的最大高度约为________m。(g取10m/s2)
23.如图是一种抛物器,轻质杠杆左端A是一个质量为M=10kg的重球,杠杆的右端是一个被抛的物体,质量为m=0.5kg,OA=OB=1m。此时杠杆与水平地面MN的夹角为θ=30°,要使其静止,则杆右端B应施加一个竖直向下的力F=________N;撤去F,杠杆逆时针转动,物体最后被竖直向上抛出,则物体上升离地面MN的最大高度约为________m。(g取10m/s2)
95,0.95
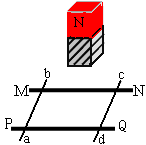 (静安) 28.如图所示,在水平面内有两条光滑平行金属轨道MN、PQ,轨道上静止放着两根质量均为m可自由运动的导体棒ab和cd。在回路的正上方有一个质量为M的条形磁铁,磁铁的重心距轨道平面高为h。由静止释放磁铁,当磁铁的重心经过轨道平面时,磁铁的速度为v,导体棒ab的动能为EK,此过程中,磁场力对磁铁所做的功
;导体棒中产生的总热量是
。
(静安) 28.如图所示,在水平面内有两条光滑平行金属轨道MN、PQ,轨道上静止放着两根质量均为m可自由运动的导体棒ab和cd。在回路的正上方有一个质量为M的条形磁铁,磁铁的重心距轨道平面高为h。由静止释放磁铁,当磁铁的重心经过轨道平面时,磁铁的速度为v,导体棒ab的动能为EK,此过程中,磁场力对磁铁所做的功
;导体棒中产生的总热量是
。
 Mv2/2―Mgh, Mgh―Mv2/2―2EK
Mv2/2―Mgh, Mgh―Mv2/2―2EK
19.(金山)一物体沿固定斜面从静止开始向下运动,经过时间t0滑至斜面底端。已知在物体运动过程中物体所受的摩擦力恒定。若用F、v、s和E分别表示该物体所受的合力、物体的速度、位移和机械能,则下列图象中可能正确的是------------------( )

A C D
(金山)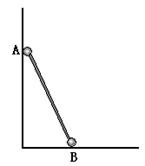 22.质量为m的物体从静止开始以g/2的加速度竖直向下运动,当下降高度为h时,该物体机械能的增量为________,该物体动能的增量为_________。
22.质量为m的物体从静止开始以g/2的加速度竖直向下运动,当下降高度为h时,该物体机械能的增量为________,该物体动能的增量为_________。
−mgh/2、 mgh/2;
(浦东) 21.在竖直平面内有一条光滑弯曲轨道,一个小环套在轨道上,从3.0m的高处无初速度释放。轨道上各个高点的高度如图所示。则第________高点是小环不可超越的;小环随后将如何运动?________________________________。

(4)、在轨道间来回作往复运动
17.(奉贤)一带电小球在从空中的a点运动到b点的过程中,重力做功3J,电场力做功1J,克服空气阻力做功0.5J,则下 列判断正确的是[ ]
列判断正确的是[ ]
A.在a点的动能比b点小3.5J B.在a点的重力势能比在b点大3J
C.在a点的电势能比在b点小1J D.在a点的机械能比在b点小0.5J
ABD
19、(嘉定)如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动。当上升高度为H时,电梯的速度达到v,则在这段过程中,下列说法中正确的是
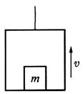 (A)电梯地板对物体的支持力所做的功等于
(A)电梯地板对物体的支持力所做的功等于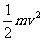
(B)电梯地板对物体的支持力所做的功大于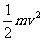
(C)钢索的拉力所做的功等于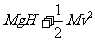
(D)钢索的拉力所做的功大于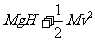
BD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com