
6.该地河谷的成因为 ( )
A.背斜顶部受到张力作用岩石破碎,河流下切侵蚀而成
B.岩层向下弯曲,河流携带泥沙沉积而成
C.岩层断裂上升,受流水侵蚀而成
D.岩层断裂下陷,洒流携带泥沙沉积而成。
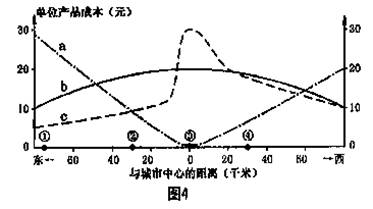 图4为某种工业部门土地、运输和劳动力等成本的曲线图。其中主地成本和运费都只与距离城市中心的远近、交通通达度有关。读图4,回答第7、8题。
图4为某种工业部门土地、运输和劳动力等成本的曲线图。其中主地成本和运费都只与距离城市中心的远近、交通通达度有关。读图4,回答第7、8题。
5.关于甲、乙、丙、丁四地农业的说法,正确的是( )
A.甲地地形平坦,可大力发展商品谷物农业
B.乙地水热充足,可种植热带经济作物
C.丙地日照强,可发展水稻种植业
D.丁地草类茂盛,可发展乳畜业
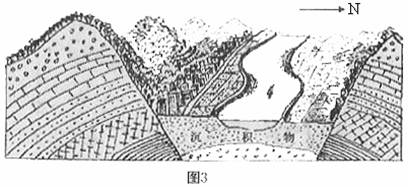 图3为我国某地地形和构造剖面图。读图3,回答第6题。
图3为我国某地地形和构造剖面图。读图3,回答第6题。
4.影响甲、乙两地年日照时数差异的主要原因是 ( )
A.地形差异 B.白昼长短差异
C.大气环流差异 D.正午太阳高度差异
3.图中 ( )
A.东岸季风气候显著,且多火山地震
B.东岸海域因只爱寒流的影响,形成了世界著名的渔场
C.甲地气温日、年差较小,典型植被为温带落叶阔叶林
D.乙地位于西北风的迎风坡,降水丰富
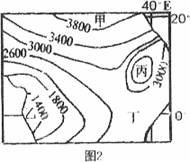 图2为某区域年日照时数等值线图。读图2,回答第4、5题。
图2为某区域年日照时数等值线图。读图2,回答第4、5题。
2.中国国际求援队于1月13日晚8时30分,乘专机从北京出发,经停温哥华飞赴海地,经过10个小时的飞行抵达温哥华机场(49°14′N,123°05′W),此时正值当地( )
A.清晨 B.午后 C.傍晚 D.深夜
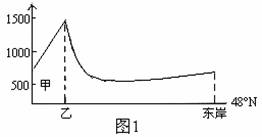 图1为某大陆北纬48°沿线地区的多年平均降水量变化示意图。读图1,回答第3题。
图1为某大陆北纬48°沿线地区的多年平均降水量变化示意图。读图1,回答第3题。
2010年初海地和智利先后发生地震。下表为两次地震的统计数据。
|
国家 |
当地时间 |
震级 (里氏) |
震源深度 (km) |
震中距首都 的距离(Km) |
死亡人数 (人) |
GDP世界 排名 |
|
海地 |
1月12日 16:53 |
7.3 |
13 |
15 |
约30万 |
134 |
|
智利 |
2月27日 3:34 |
8.8 |
35 |
325 |
约750 |
56 |
读上表,回答第1、2题。
1.两次地震造成人员伤亡不同,主要原因有 ( )
①震级大小不同 ②震源深度不同 ③人口密度差异
④发生时间不同 ⑤经济实力差异
A.①②③ B.①③⑤ C.②③④ D.②③⑤
20.(14分)
设集合W由满足下列两个条件的数列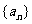 构成:
构成:
①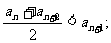
②存在实数M,使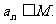 (n为正整数)
(n为正整数)
(I)在只有5项的有限数列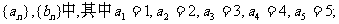
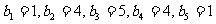 ;试判断数列
;试判断数列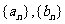 是否为集合W的元素;
是否为集合W的元素;
(II)设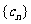 是各项为正的等比数列,
是各项为正的等比数列,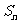 是其前n项和,
是其前n项和,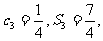 证明数列
证明数列 ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列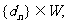 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有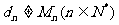 .
.
求证:数列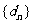 单调递增.
单调递增.
19.(13分)
在直角坐标系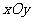 中,点M到点
中,点M到点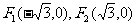 的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线
的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线 与轨迹C交于不同的两点P和Q.
与轨迹C交于不同的两点P和Q.
(I)求轨迹C的方程;
(II)当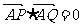 时,求k与b的关系,并证明直线
时,求k与b的关系,并证明直线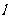 过定点.
过定点.
18.(13分)
已知函数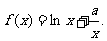
(I)当a<0时,求函数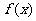 的单调区间;
的单调区间;
(II)若函数f(x)在[1,e]上的最小值是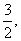 求a的值.
求a的值.
17.(14分)
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为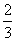 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为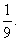
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为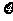 ,求
,求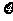 的分布列与均值E
的分布列与均值E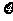 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com