
17.如图在△ABC中角 A,B,C 所对的边分别是a ,b,c,且a=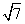 b=2,c=3.O为△ABC的外心
b=2,c=3.O为△ABC的外心
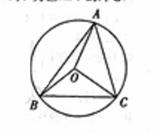 (1)求
(1)求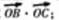
(2)求△ABC面积
6.若随机变量 服从正态分布
服从正态分布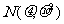 ,关于命题:
,关于命题:
(1)正态曲线关于直线x=对称
(2)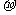 越小,正态曲线越‘矮胖’;
越小,正态曲线越‘矮胖’; 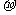 越大,正态曲线越‘瘦高’
越大,正态曲线越‘瘦高’
(3)以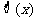 表示标准正态总体在区间(
表示标准正态总体在区间(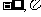 )内取值的概率,则概率
)内取值的概率,则概率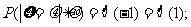
(4)若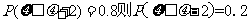
正确的是______(写出所有正确命题的序号)
三 解答题 :本大题共6小题,第17题10分第18-22每题12分,解答应写出文字说明,证明过程活演算步骤。
15.已知动点P(x,y)在椭圆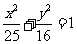 上,若A(3,0),
上,若A(3,0),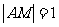 ,且
,且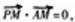 ,则
,则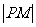 的最小值是_____
的最小值是_____
14.已知数列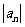 中,
中,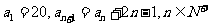 则数列
则数列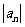 的通项公式是______
的通项公式是______
13.设变量x.y 高 考 资 源 网满足约束条件 ,则目标函数z=2x+4y的最大值为______
,则目标函数z=2x+4y的最大值为______
12.已知f(x)是定义在R上且以2为周期的偶函数,当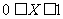 时
时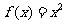 。如果直线y=x+a与曲线y=f(x)恰有两个交点,则实数a的值是
。如果直线y=x+a与曲线y=f(x)恰有两个交点,则实数a的值是
A 0 B 2k(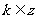 ) C2k或
) C2k或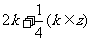 D 2k或
D 2k或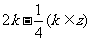
第⑾卷
二填空题
11.已知抛物线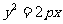 (p>0)与双曲线
(p>0)与双曲线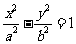 (a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则高 考 资 源 网双曲线的离心率
(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则高 考 资 源 网双曲线的离心率
A 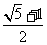 B
B 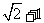 C
C
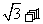 D
D 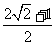
10.一个正四棱柱的底面边长为8,高为6,在其内部的底面上放入四个大小相同的球,使相邻的两球彼此相切,并且都与相邻的侧面相切,在四个球的上面在放一个球,使这个球在正四棱柱内部,则这个球的半径在最大值( )
A 2 B 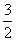 C
C 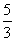 D
D 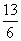
9.已知一个平面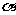 ,那么对于空间内的任意一条直线a,在平面
,那么对于空间内的任意一条直线a,在平面 内一定存在一条直线b,使得a与b ( )
内一定存在一条直线b,使得a与b ( )
A 平行 B 相交 C 异面 D垂直
7.设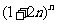 展开式的各项系数的和为
展开式的各项系数的和为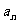 ,各二项式系数的和为
,各二项式系数的和为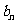 则
则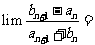
A  B
B  C -1 D 0
C -1 D 0
8. 某市第三中学要从4名男生和3名女生中选派4人参加北京大学‘自主招生夏令营’活动,若这4人中至少有一名女生,则不同的选派方案有
A 25 B 35 C34 D 816
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com