
20. (本小题满分13分)
已知数列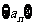 满足:
满足: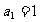 ,
,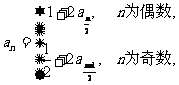 ,
, 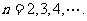
(Ⅰ)求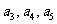 的值;
的值;
(Ⅱ)设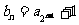 ,
,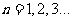 ,求证:数列
,求证:数列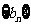 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III)对任意的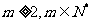 ,在数列
,在数列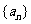 中是否存在连续的
中是否存在连续的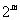 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这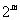 项,并证明这
项,并证明这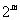 项构成等差数列;若不存在,说明理由.
项构成等差数列;若不存在,说明理由.
海淀区高三年级第二学期期中练习
19. (本小题满分13分)
已知椭圆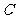 的对称中心为原点O,焦点在
的对称中心为原点O,焦点在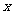 轴上,离心率为
轴上,离心率为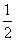 , 且点(1,
, 且点(1,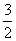 )在该椭圆上.
)在该椭圆上.
(I)求椭圆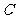 的方程;
的方程;
(II)过椭圆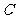 的左焦点
的左焦点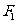 的直线
的直线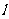 与椭圆
与椭圆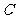 相交于
相交于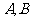 两点,若
两点,若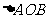 的面积为
的面积为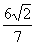 ,求圆心在原点O且与直线
,求圆心在原点O且与直线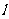 相
相 切的圆的方程.
切的圆的方程.
18. (本小题满分14分)
已知函数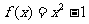 与函数
与函数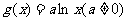 .
.
(I)若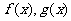 的图象在点
的图象在点 处有公共的切线,求实数
处有公共的切线,求实数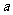 的值;
的值;
(II)设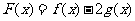 ,求函数
,求函数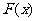 的极值.
的极值.
17. (本小题满分14分)
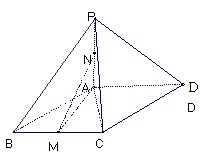
如图:在四棱锥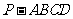 中,底面
中,底面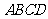 是菱形,
是菱形,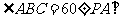 平面ABCD,
平面ABCD,
 点
点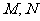 分别为
分别为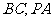 的中点,且
的中点,且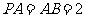 .
.
(I) 证明: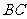
 ⊥平面
⊥平面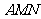 ;
;
(II)求三棱锥
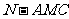 的体积;
的体积;
(III)在线段PD上是否存在一点E,使得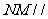 平面
平面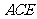 ;若存在,求出PE的长;若不存在,说明理由.
;若存在,求出PE的长;若不存在,说明理由.
16. (本小题满分13分)
(本小题满分13分)
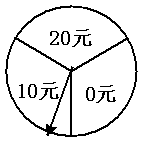
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等. 假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了218元 ,第一次转动获得了20元,第二次获得了10元,则其共获得了30元 优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
(I )若顾客甲消费了128元,求他获得优惠券面额大于0元的概率?
)若顾客甲消费了128元,求他获得优惠券面额大于0元的概率?
(II)若顾客乙消费了280元,求他总共获得优惠券金额不低于20元的概率?
15. (本小题满分13分)
已知函数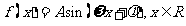 (其中
(其中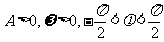 ),
),
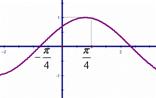 其部分图象如图所示.
其部分图象如图所示.
(I)求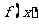 的解析式;
的解析式;
(II)求函数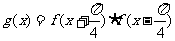 在区间
在区间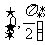 上的
上的
最大值及相应的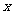 值.
值.
14. 若点集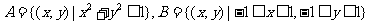 ,则(1)点集
,则(1)点集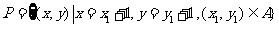 所表示的区域的面积为_____;
所表示的区域的面积为_____;
(2)点集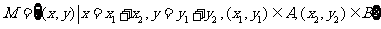 所表示的区域的面积为___________ .
所表示的区域的面积为___________ .
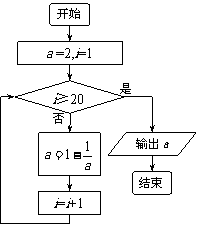
13. 已知程序框图如图所示,则执行该程序后输出的结果是_______________.
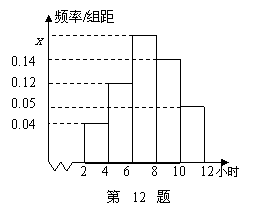
12. 某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的同学为 _______人.
某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的同学为 _______人.
 |
|||
|
11. 已知不等式组 , 表示的平面区域的面积为4,点
, 表示的平面区域的面积为4,点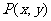 在所给平面区域内,
在所给平面区域内,
则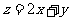 的最大值为______.
的最大值为______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com