
22.已知函数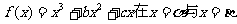 处有两上不同的极值点,设
处有两上不同的极值点,设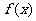 在点
在点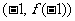 处切线为
处切线为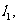 其斜率为
其斜率为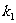 ;在点
;在点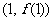 利的切线为
利的切线为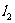 ,其斜率为
,其斜率为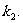
(1)若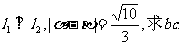
(2)若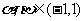 ,求
,求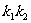 可能取到的最大整数值。
可能取到的最大整数值。
21.已知过点A(-4,0)的动直线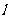 与抛物线
与抛物线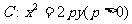 相交于B、C两点。当
相交于B、C两点。当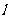 的斜率是
的斜率是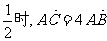 。
。
(1)求抛物线C的方程;
(2)设BC的中垂线在y轴上的截距为b,求b的取值范围。
20.如图,三棱柱ABC-A1B1C1,侧棱与底面垂直,P,Q分别是棱BB1,CC1上的点,AB⊥A1Q,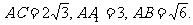
(1)求证:AC⊥A1P;
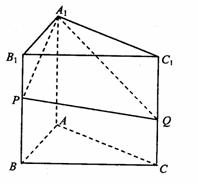 (2)若M是
(2)若M是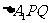 的重心,AM⊥面A1PQ,求平面A1PQ与面BCC1B1所成角(锐角)的余弦值。
的重心,AM⊥面A1PQ,求平面A1PQ与面BCC1B1所成角(锐角)的余弦值。
19.从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同。
(1)若抽取后又放回,抽3次,分别求恰2次为红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,抽完红球所需次数为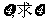 的分布列及期望。
的分布列及期望。
18.已知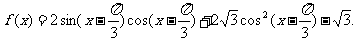
(1)求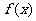 的最大值及取得最大值时相应的x的值;
的最大值及取得最大值时相应的x的值;
(2)若函数 上恰有两上零点
上恰有两上零点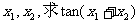 的值。
的值。
17.球O与正方体ABCD-A1B1C1D1各面都相切,P是球O上一动点,AP与面ABCD所成角为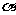 ,则
,则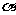 最大时,其正切值为
。
最大时,其正切值为
。
16.若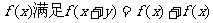 ,则可写出满足条件的一个函数解析式
,则可写出满足条件的一个函数解析式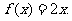 类比可以得到:若定义在R上的函数
类比可以得到:若定义在R上的函数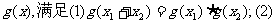
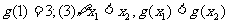 ,则可以写出满足以上性质的一个函数解析式为
,则可以写出满足以上性质的一个函数解析式为
。
15.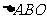 三顶点坐标为A(1,0),B(0,2),O(0,0),P(x,y)是坐标平面内一点,满足
三顶点坐标为A(1,0),B(0,2),O(0,0),P(x,y)是坐标平面内一点,满足 ,
,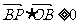 ,则
,则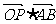 的最小值为 。
的最小值为 。
14.圆C的半径为1,圆心在第一象限,与y轴相切,与x轴相交于A、B,|AB|=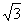 ,则该圆的标准方程是
。
,则该圆的标准方程是
。
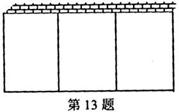
13.有一批材料可以建成200m长的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样材料同成三个面积相等的矩形(如图所示),则围成场地的最大面
积为 (围墙厚度不计)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com