
53、 如图所示,质量m=1kg的小球套在细斜杆上,斜杆与水平方向成a=30°角,球与杆之间的滑动摩擦因数m=
如图所示,质量m=1kg的小球套在细斜杆上,斜杆与水平方向成a=30°角,球与杆之间的滑动摩擦因数m=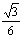 ,球在竖直向上的拉力F=20N作用下沿杆向上滑动.g取10m/s2.
,球在竖直向上的拉力F=20N作用下沿杆向上滑动.g取10m/s2.
(1)在右中画出小球的受力图.
(2)求球对杆的压力大小和方向.
(3)小球的加速度多大?
(1)小球受力如图所示. (2分)
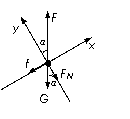 (2)建立图示坐标系,沿y方向:
(2)建立图示坐标系,沿y方向:
(F-mg)cos30°-FN=0 (2分)
解得 FN=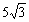 N (2分)
N (2分)
根据牛顿第三定律,球对杆的压力大小为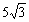 N,方向垂直于杆向上 (2分)
N,方向垂直于杆向上 (2分)
(3)沿x方向由牛顿第二定律得
(F-mg)sin30-f=ma (2分)
而 f=m FN (2分)
解得 a=2.5m/s2 (2分)
52、用一沿斜面向上的恒力F将静止在斜面底端的物体向上推,推 到斜面中点时,撤去F,物体正好运动到斜面顶端并开始返回。在此情况下,物体从底端到顶端所需时间为t,从顶端滑到底端所需时间也为t。若物体回到底端时速度为10m/s,试问:(1)推力F与物体所受斜面摩擦力Ff之比为多少?(2)斜面顶端和底端的高度差h为多少?
到斜面中点时,撤去F,物体正好运动到斜面顶端并开始返回。在此情况下,物体从底端到顶端所需时间为t,从顶端滑到底端所需时间也为t。若物体回到底端时速度为10m/s,试问:(1)推力F与物体所受斜面摩擦力Ff之比为多少?(2)斜面顶端和底端的高度差h为多少?
解 析:设物体的质量为m,在F作用下的加速度大小为a1 ,到达中点速度为v ,撤去F后上滑的加速度大小为a2 ,下滑的加速度大小为a3 ,斜面的倾角为θ,斜面的长度为s, 根据牛顿第二定律,有上滑过程: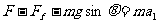
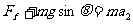
下滑过程: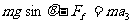
由运动学公式: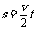
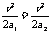

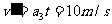
又 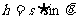
联立上述各式,解得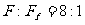 h=7.5m
h=7.5m
51、 固定光滑细杆与水平地面成一定倾角,在杆上套有一个光滑小环,小环在沿杆方向向上的推力 F 作用下向上运动. 0 一 2s内推力的大小为 5 .0N
, 2 一 4s
固定光滑细杆与水平地面成一定倾角,在杆上套有一个光滑小环,小环在沿杆方向向上的推力 F 作用下向上运动. 0 一 2s内推力的大小为 5 .0N
, 2 一 4s  内推力的大小变为 5.5N ,小环运动的速度,随时间变化规律如图所示,取重力加速度 g = 10 m/s 2
.求:
内推力的大小变为 5.5N ,小环运动的速度,随时间变化规律如图所示,取重力加速度 g = 10 m/s 2
.求:
( l )小环在加速运动时的加速度 a 的大小; ( 2 )小环的质量 m ; ( 3 )细杆与水平地面之间的夹角 α .
①a=0.5m/s2 ②m=1kg ③α=300
50、质量为M=10kg的B板上表面上方,存在一定厚度的相互作用区域,如图中划虚线的部分,当质量为m=1kg的物块P进入相互作用区时,B板便有竖直向上的恒力f= kmg(k=51)作用于物块P,使其刚好不与B板的上表面接触;在水平方向,物块P与B板间没有相互作用力. 已知物块P开始自由下落的时刻,B板向右运动的速度为VBo=10m/s. 物块P从开始下落到刚到达相互作用区所经历的时间为t0=2.0s. 设B板足够长,B板与水平面间的动摩擦因数μ=0.02,为保证物块P总能落入B板上方的相互作用区,问:(1)物块P从起始位置下落到刚好与B板不接触的时间 t
(2)物块B在上述时间t内速度的改变量
(3)当B板刚好停止运动时,物块P已经回到过初始位置几次?(g=10m/s2)
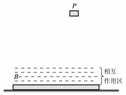 解:(1)物块P刚到达相互作用区时的速度
解:(1)物块P刚到达相互作用区时的速度
VO=gto (1)(1分)
物块P进入相互作用后的加速度
a1= (kmg-mg)/m=(k-1)g (2)(1分)
解(1)(2)得物块P在相互作用 区内的运动时间
区内的运动时间
t1=v0/a1=0.04s (3)(1分)
物块P从起始位置下落到刚好与B不接触时的运动时间
t=t0+t1=2.04s (4)(2分)
(2)板B在物块P未进入作用区时的加速度
aB1=μg (5)(1分)
速度的改变量Δvb1 = aB1t0 =0.4m/s (6)(1分)
当物块P进入作用区后的加速度
aB2 =μ(Mg+kmg)/M (7)(1分)
由(3)(7)得速度的改变量
Δvb2 = aB2t1=0.0488m/s (8) (1分)
所以:板B在物块P从起始位置下落到刚好与B不接触时
由(6)(8)得:速度的改变量
Δv=Δv b1+Δv b2 =0.4488m/s (9) (2分)
(3)当物块P的速度减到零后,又开始以加速度a向上做加速运动,经历时间t1,跑出相互作用区,在这段时间内,B板减少的速度仍是Δvb2;物块P离开相互作用区后,做加速度为g的减速运动,经历时间t0,回到初始位置,在这段时间内,B板减少的速度为Δvb1,以后物块又从起始位置自由落下,重复以前的运动,B板的速度再次不断减少.总结以上分析可知:每当物块P完成一次从起始位置自由下落,进入相互作用区后又离开相互作用区,最后回到起始位置的过程中,B板速度减少的总量为
Δv=2Δv b1+2Δv b2 =0.8978m/s (10) 2分
设在物块P第n次回到起始位置,
n=vBo/Δv=10/0.8978=11.11≈11次 (11) (2分)
49、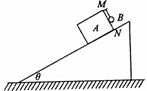 如图所示,固定在水平面上的斜面倾角θ=37°,长方体木块A的MN面上钉着一颗小钉子,质量m=1.5kg的小球B通过一细线与小钉子相连接,细线与斜面垂直,木块与斜面间的动摩擦因数μ=0.50.现将木块由静止释放,木块将沿斜面下滑.求在木块下滑的过程中小球对木块MN面的压力.(取g=10m/s2, sin37°=0.6, cos37°=0.8)
如图所示,固定在水平面上的斜面倾角θ=37°,长方体木块A的MN面上钉着一颗小钉子,质量m=1.5kg的小球B通过一细线与小钉子相连接,细线与斜面垂直,木块与斜面间的动摩擦因数μ=0.50.现将木块由静止释放,木块将沿斜面下滑.求在木块下滑的过程中小球对木块MN面的压力.(取g=10m/s2, sin37°=0.6, cos37°=0.8)
解:由于木块与斜面间有摩擦力的作用,所以小球B与木块间有压力的作用,并且它们以共同的加速度a沿斜面向下运动.将小球和木块看作一个整体,设木块的质量为M,根据牛顿第二定律可得
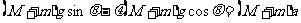 (4分)
(4分)
代入数据得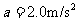 (3分)
(3分)
选小球为研究对象,设MN面对小球的作用力为N,
根据牛顿第二定律有 (4分)
(4分)
代入数据得 (2分)
(2分)
根据牛顿第三定律,小球对MN面的压力大小为6.0N,方向沿斜面 (1分)
48、 长L是1m,质量M是2kg的长方形木板A放在光滑的水平面上,在木板的左端放置一个质量m是1kg的物块B。A与B之间的动摩擦因数μ是0.2,现用一个F为8N的水平恒力向右拉B。
长L是1m,质量M是2kg的长方形木板A放在光滑的水平面上,在木板的左端放置一个质量m是1kg的物块B。A与B之间的动摩擦因数μ是0.2,现用一个F为8N的水平恒力向右拉B。
(1)要使B从A的右端滑出,则力F至少要做多少功?
 (2)若M、m、μ、F中某一物理量发生变化,拉出过程中做功的最小值也会变化。要使拉出过程中做功的最小值变小,应采用哪些方法?(只要说出两种,每种方法中只允许改变M、m、μ、F中的一个
(2)若M、m、μ、F中某一物理量发生变化,拉出过程中做功的最小值也会变化。要使拉出过程中做功的最小值变小,应采用哪些方法?(只要说出两种,每种方法中只允许改变M、m、μ、F中的一个 ,并说出此物理量变大还是变小)
,并说出此物理量变大还是变小)
(1)设力F作用时间为t1,则
a B=F-μmg/m =6m/s2 (1分)
aA=μmg/M=1m/s2 (1分)
相对运动距离△S1=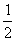 (a B - aA)t12 (1分)
(a B - aA)t12 (1分)
设撤去F时B的速度为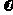 B、A的速度为
B、A的速度为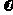 A。经t2时间后 B正好滑到右端且速度与A相同
A。经t2时间后 B正好滑到右端且速度与A相同
aB'=μg=2m/s2 方向向左
aA'=aA=1m/s2
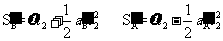
相对运动距离△S2=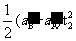 (1分)
(1分)
由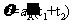
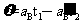
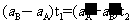 (1分)
(1分)
得t2 =5t1/3 (1分)
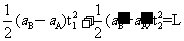 (1分)
(1分)
t1=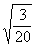 s
(1分)
s
(1分)
WF=F·SB=F·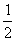 aBt12
(1分)
aBt12
(1分)
WF==3.6J (1分)
(2)M变大、m变小、μ变小、F变大(只答一个且正确得1分;答两个或两个以上的,全部正确得3分,有错的不得分)
47、如图所示,质量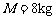 的小车放在光滑水平面上,在小车右端施加一水平恒力
的小车放在光滑水平面上,在小车右端施加一水平恒力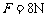 .当小车向右运动速度达到3m/s时,在小车的右端轻轻放上一质量
.当小车向右运动速度达到3m/s时,在小车的右端轻轻放上一质量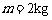 的小物块,物块与小车间的动摩擦因数
的小物块,物块与小车间的动摩擦因数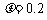 ,小物块始终不离开小车,问:
,小物块始终不离开小车,问:
(1)小车至少要多长?
 (2)小物块从放在小车上开始计时,经过3s时间,摩擦力对小物块做的功
(2)小物块从放在小车上开始计时,经过3s时间,摩擦力对小物块做的功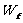 和拉力
和拉力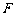 对小车做的功
对小车做的功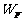 分别是多少?(
分别是多少?(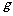 取10m/s2)
取10m/s2)

46、如图(a)所示,质量为M = 10kg的滑块放在水平地面上,滑块上固定一个轻细杆ABC,∠ABC = 45°.在A端固定一个质量为m = 2kg的小球,滑块与地面间的动摩擦因数为m = 0.5.现对滑块施加一个水平向右的推力F1 = 84N,使滑块做匀加速运动.求此时轻杆对小球作用力F2的大小和方向.(取g=10m/s2)
有位同学是这样解的--
小球受到重力及杆的作用力F2,因为是轻杆,所以F2方向沿杆向上,受力情况如图(b)所示.根据所画的平行四边形,可以求得:
F2 =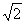 mg =
mg = 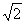 ×2×10N = 20
×2×10N = 20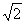 N.
N.
你认为上述解法是否正确?如果不正确,请说明理由,并给出正确的解答.

结果不正确.…………………………………………………………………………(2分)
杆AB对球的作用力方向不一定沿着杆的方向,它可能会是右向上的方向.大小和方向具体由加速度a的大小来决定.并随着加速度a的变化而变化.………………(2分)
由牛顿第二定律,对整体有 F-μ(M+m)g=(M+m)a ………………………(2分)
解得a=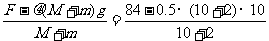 m/s2
= 2 m/s2………………(1分)
m/s2
= 2 m/s2………………(1分)
F2 = 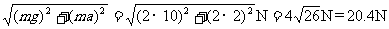 …………(1分)
…………(1分)
轻杆对小球的作用力F2与水平方向夹角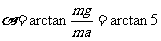 ,斜向右上.(2分)
,斜向右上.(2分)
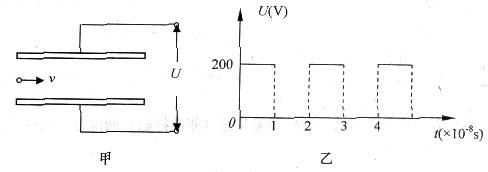
57、两平行金属板长L=O.1m,板间距离d=l×10-2m,从两板左端正中间有带电粒子持续飞入,如图甲所示.粒子的电量q=10-10c,质量m=10-20kg,初速度方向平行于极板,大小为v=10 7m/s,在两极板上加一按如图乙所示规律变化的电压,不计带电粒子 重力作用.求:
(1)带电粒子如果能从金属板右侧飞出,粒子在电场中运动的时间是多少?
(2)试通过计算判断在t=1.4×10--8s和t=0.6×10--8s时刻进入电场的粒子能否飞出.
(3)若有粒子恰好能从右侧极板边缘飞出,该粒子飞出时动能的增量△EK=?
(16分)参考解答及评分标准 。
(1)粒子在电场中飞行的时间为t则 .
t=L/v ……………………(2分) .
代入数据得:.t=1×1 0-8S ……(2分) 。 ‘
(2)粒子在电场中运动的加速度a=Eq/m=qU/md=2 X l 0 14m/s2 .
当t=1.4×1 O-8s时刻进入电场,考虑竖直方向运动,前0.6×1 0-8s无竖直方向位移,后0.4×10 -8s做匀加速运动。竖直方向位移
Sy=1/2at2=0.16×10-2m<d/2=0.5×10-2m …………………… (2分)
∴能飞出两板间 (1分)
当t=-O.6×1 O-8s时刻进入电场,考虑竖直方向运动,前0.4×1 0-8s匀加速运动,后O.6×1 O-8s
做匀速运动。竖直方向位移 .
Sy'=s1+s2=1/2at2+at(T-t)=0.64 x10-2m>d/2=0.5×10-2m…………………… (2分)
∴不能飞出两板间 …………………… (1分)
(3)若粒子恰能飞出两板间,考虑两种情况
a.竖直方向先静止再匀加速。
Sy=1/2at2 0.5×1 0-2=l/2 ×2 ×10 14t2
得t= 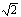 /2×1 0-8s
…………………… (1分)
/2×1 0-8s
…………………… (1分)
∴ ΔEk=Uq/2=I×1 0-8J …………………… (2分)
b.竖直方向先匀加速再匀速
Sy = S1+S2 =
1/2at2 + at(T-t) 0.5 X  1 0-2=1/2X2X10 14 t2+2
X 10 14t(1×1 0-8-t)
1 0-2=1/2X2X10 14 t2+2
X 10 14t(1×1 0-8-t)
得t = (1-√2/2)X×1 0-8S
∴S1=1/2at2 = (1.5一√2)×10-2m …………………… (1.分)
∴ΔEk=EqS1=UqS1/d=(3-2√2)×1 0一8=0.1 7 X 1 0-8j …………………… (2分)
56、在光滑绝缘的水平面上,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的带电量为+2q,B球的带电量为-3q,组成一带电系统,如图所示,虚线MP为AB两球连线的垂直平分线,虚线NQ与MP平行且相距4L.最初A和B分别静止于虚线MP的两侧,距MP的距离均为L,且A球距虚线NQ的距离为3L.若视小球为质点,不计轻杆的质量,在虚线MP, NQ间加上水平向右的匀强电场E后,求:
(1)B球刚进入电场时,带电系统的速度大小.
 (2)带电系统从开始运动到速度第一次为零所需时间以及B球电势能的变化量.
(2)带电系统从开始运动到速度第一次为零所需时间以及B球电势能的变化量.
 解: ⑴带电系统开始运动时,设加速度为a1,由牛顿第二定律:
解: ⑴带电系统开始运动时,设加速度为a1,由牛顿第二定律:
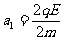 =
=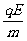 (2分)
(2分)
球B刚进入电场时,带电系统的速度为v1, 有:
有:
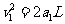 求得:
求得: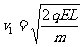 (2分)
(2分)
⑵对带电系统进行分析,假设球A能达到右极板,电场力对系统做功为W1,有:
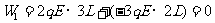
故带电系统速度第一次为零时,球A恰好到达右极板Q。 (2分)
设球B从静止到刚进入电场的时间为t1,则:
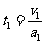 解得:
解得: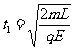 (1分)
(1分)
球B进入电场后,带电系统的加速度为a2,由牛顿第二定律:
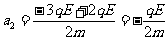 (2分)
(2分)
显然,带电系统做匀减速运动。减速所需时间为t2,则有:
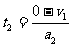 求得:
求得: 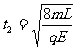 (2分)
(2分)
可知,带电系统从静止到速度第一次为零所需的时间为:
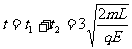 (1分)
(1分)
B球电势能增加了 6 Eq L (2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com