
7.已知直线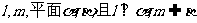 ,给出下列四个命题
,给出下列四个命题
①若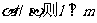 ; ②若
; ②若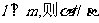 ;
;
③若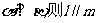 ; ④若
; ④若
其中正确命题的个数是 ( )
A.0 B.1 C.2 D.3
6.大小相同的4个小球上分别写有数字1,2,3,4,从这4个小球中随机抽取2个小球,则取出的2个小球上的数字之和为奇数的概率为` ( )
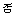
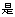

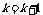
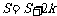
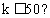
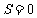







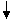
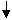
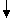
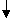





 A.
A.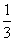 B.
B.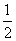 C.
C.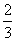 D.
D.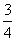
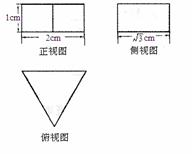
5.某个几何体的三视图如图所示,则该几何体的体积是( )
A.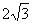 B.
B.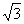
C.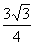 D.
D.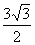
3.在复平面内,复数z=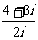 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
|
 4.定义:
4.定义: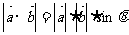 ,其中
,其中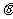 为向量
为向量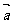 与
与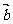 的夹角,若
的夹角,若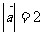 ,
,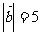 ,
,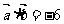 ,则
,则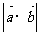 等于 ( )
等于 ( )
A.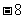 B.
B.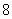 C.
C.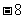 或
或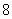 D.
D.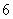
2.已知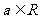 ,则“
,则“ ”是“
”是“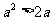 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.设集合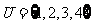 ,
, 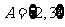 ,
, 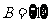 , 则
, 则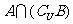 等( )
等( )
A. 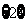 B.
B.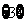 C.
C.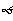 D.
D.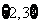
57、一位质量为60kg的跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当下落到距离地面125m高处时立即打开降落伞,在减速下落的过程中,运动员受到伞绳的拉力恒为1458N,到达地面时的速度为5m/s,重力加速度g取10m/s2,在不考虑风力和运动员所受空气阻力情况下,求:
(1)运动员离开飞机时距地面的高度.
(2)离开飞机后,运动员经过多少时间才能到达地面.
解:(1)设运动员减速下落时的加速度为a,由牛顿第二定律得:
F-mg = ma ① (2分)
由运动学公式得:
v2-v02 =2ax ② (1分)
运动员自由下落的时间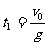 ③ (1分)
③ (1分)
下落的高度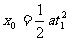 ④ (1分)
④ (1分)
运动员离开飞机时距地面的高度H = x0+x ⑤ (1分)
v0=60m/s ⑥
由①②③④⑤式求得H=305m . (1分)
(2)运动员减速向下运动的时间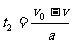 ⑦ (1分)
⑦ (1分)
离开飞机后,经过t时到达地面,t = t1+t2 ⑧ (1分)
由⑥⑦⑧式得t = 9.8s. (1分)
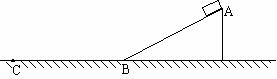
56、如图所示,斜面倾角为37°(sin37°=0.6,cos37°=0.8),一木块从斜面顶端A由静止开始下滑,当滑到B时进入水平面滑行到C点停止。已知木块与斜面和水平面之间的动摩擦因数相同,AB和BC间的距离相等,且为S。不计木块从斜面底端进入水平面时的机械能损 失。
失。
(1)木块与斜面和水平面之间的动摩擦因数μ是多大?
(2)若S=5m,则木块刚进入水平面时的速度是多大?
解:⑴
mgsin37°-μmgcos37°=ma1 ①
由υ2-0=2a1s , 0-υ2=2a2s 得: [来源:ZXXK]
2a1s=-2a2s ②
-μmg=ma2 ③
解①②③式得:
μ=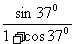 =
=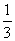 ④
④
⑵解③④式得
a2=-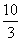 m/s2
⑤
m/s2
⑤
由0-υ2=2a2s得:
υ= =
=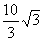 m/s
⑥
m/s
⑥
评分标准:①②⑤各2分,③④⑥各1分
55、在消防演习中,消防队员从一根竖直的长直轻绳上由静止滑下,经一段时间落地.为了获得演习中的一些数据,以提高训练质量,研究人员在轻绳上端安装一个力传感器并与数据处理系统相连接,用来记录消防队员下滑过程中轻绳受到的拉力与消防队员重力的比值随时间变化的情况.已知某队员在一次演习中的数据如图所示,求该消防队员在下滑过程中的最大速度和落地速度各是多少?g取10m/s2.
解:该队员先在t1=1s时间内以a1匀加速下滑.
然后在t2=1.5s时间内以a2匀减速下滑.
第1s由牛顿第二定律得:mg-F1=ma1 (2分)
所以a1=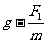 =4m/s2
(1分)
=4m/s2
(1分)
最大速度vm=a1t1
代入数据解得:vm=4m/s (2分)
后1.5s由牛顿第二定律得:F2-mg=ma2 (2分)
a2=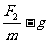 =2m/s2
(1分)
=2m/s2
(1分)
队员落地时的速度v=vm-a2t2
代入数据解得:v=1m/s (2分)
54、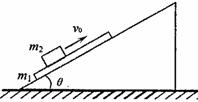 如图所示,倾角为θ的光滑斜面上放有一个质量为m1的长模板,当质量为m2的物块以初速度v0在木板上平行斜面向上滑动时,木板恰好相对斜面体静止。已知物块在木板上滑的整个过程中,斜面体相对底面没有滑动。求:
如图所示,倾角为θ的光滑斜面上放有一个质量为m1的长模板,当质量为m2的物块以初速度v0在木板上平行斜面向上滑动时,木板恰好相对斜面体静止。已知物块在木板上滑的整个过程中,斜面体相对底面没有滑动。求:
(1)物块沿木板上滑过程中,鞋面题受到底面的摩擦力;
(2)物块沿木板上滑过程中,物块由速度v0变为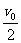 时所通过的距离
时所通过的距离

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com