
4.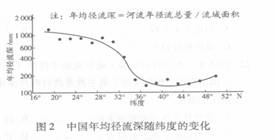 读图2,下列叙述正确的是
读图2,下列叙述正确的是
A.年均径流深随纬度增大而递减
B.年均径流深的最大值在海南省
C.年均径流深与降水量年际变化的
空间分布特点一致
D.年均径流深与蒸发量随纬度变化
的分布特点一致
自2009年秋季至今,我国西南地区遭遇旱灾,局部地区遭遇百年一遇的严重旱灾。据
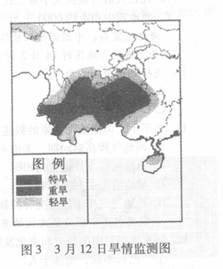 图3回答5、6题。
图3回答5、6题。
3.银川平原自古以来就是重要农业区,其主要原因是
A.光热充足 B.地势低平
C.水源丰富 D.历史悠久
2.银川平原的形成原因是
A.地壳下沉,风力沉积
B.断裂下沉,冰川物质堆积
C.地壳抬升,河流侵蚀
D.断裂下沉,黄河泥沙沉积
1. 贺兰山成为“绿岛”的主要原因是
贺兰山成为“绿岛”的主要原因是
A.太阳辐射强,热量充足
B.地形抬升,降水较多
C.冰川融水多,水源充足
D.土层深厚,植被茂密
20.(本小题满分14分)
已知数列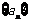 满足:
满足: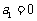 ,
,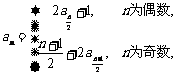 ,
,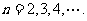
(Ⅰ)求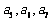 的值;
的值;
(Ⅱ)设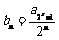 ,试求数列
,试求数列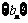 的通项公式;
的通项公式;
(Ⅲ)对于任意的正整数n,试讨论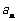 与
与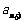 的大小关系.
的大小关系.
海淀区高三年级第二学期期中练习
数 学  (理)
(理)
19.(本小题满分13分)
已知椭圆C的中心在原点,焦点在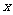 轴上,左右焦点分别为
轴上,左右焦点分别为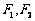 ,且
,且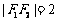 ,点(1,
,点(1,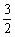 )
)
在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过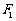 的直线
的直线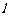 与椭圆
与椭圆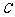 相交于
相交于 两点,且
两点,且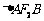 的面积为
的面积为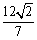 ,求以
,求以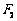 为圆心
为圆心
且与直线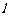 相切的圆的方程.
相切的圆的方程.
18.(本小题满分13分)
已知函数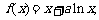 其中a为常数,且
其中a为常数,且 .
.
(Ⅰ)当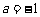 时,求
时,求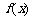 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若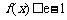 对任意
对任意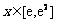 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
17.(本小题满分14分)
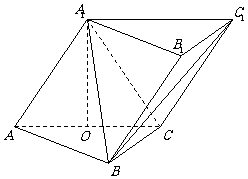
如图,三棱柱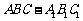 中,侧面
中,侧面
 底面
底面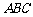 ,
,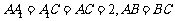 ,
,
且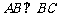 ,O为
,O为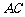 中点.
中点.
(Ⅰ)证明: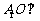 平面
平面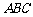 ;
;
(Ⅱ)求直线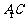 与平面
与平面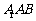 所成角的正弦值;
所成角的正弦值;
 (Ⅲ)在
(Ⅲ)在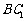 上是否存在一点
上是否存在一点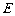 ,使得
,使得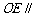 平面
平面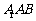 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点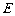 的位置.
的位置.
16.(本小题满分13分)
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;
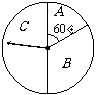
(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为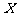 (元).求随机变量
(元).求随机变量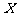 的分布列和数学期望.
的分布列和数学期望.
15.(本小题满分13分)
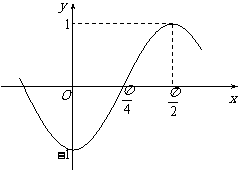
已知函数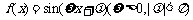 的图象如图所示.
的图象如图所示.
(Ⅰ)求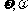 的值;
的值;
(Ⅱ)设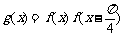 ,求函数
,求函数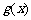 的单调递增区间.
的单调递增区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com