
6.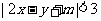 等价于
等价于
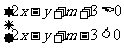
画图可知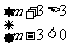 ,故
,故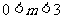 .所以选C
.所以选C
5. ,所以选C.
,所以选C.
4.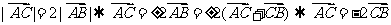 或
或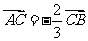 ,所以选C.
,所以选C.
3.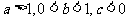 ,所以选
,所以选 .
.
1.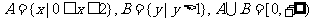 ,所以选B.
,所以选B.
2依题意得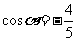 。又
。又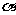 在第二象限,所以
在第二象限,所以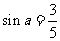 ,
,
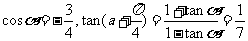 ,故选C
,故选C
22.已知函数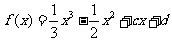 有极值.
有极值.
(Ⅰ)求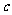 的取值范围;
的取值范围;
(Ⅱ)若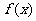 在
在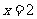 处取得极值,且当
处取得极值,且当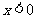 时,
时,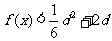 恒成立,求
恒成立,求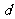 的取值范围.
的取值范围.
21.(本小题满分12分)
已知椭圆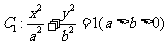 的左、右焦点分别为
的左、右焦点分别为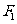 、
、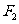 ,其中
,其中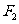 也是抛物线
也是抛物线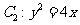 的焦点,
的焦点,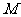 是
是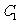 与
与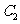 在第一象限的交点,且
在第一象限的交点,且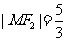 .
.
(1)求椭圆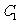 的方程;
的方程;
(2)已知菱形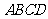 的顶点
的顶点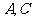 在椭圆
在椭圆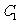 上,顶点
上,顶点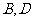 在直线
在直线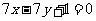 上,求直线
上,求直线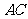 的方程.
的方程.
20.(本小题满分12分)
已知数列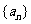 、
、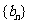 满足
满足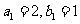 ,且
,且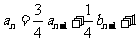 ,
,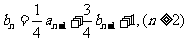
(1)令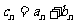 ,求数列
,求数列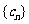 的通项公式;
的通项公式;
(2)求数列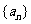 的通项公式及前
的通项公式及前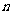 项和公式
项和公式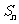 .
.
19.(本小题满分12分)如图,四棱锥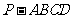 中,侧面PDC是边长为2的正三角形,且与底面
中,侧面PDC是边长为2的正三角形,且与底面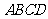 垂直,底面ABCD是面积为
垂直,底面ABCD是面积为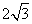 的菱形,
的菱形,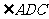 为锐角,M为PB的中点。
为锐角,M为PB的中点。
(1)求证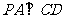
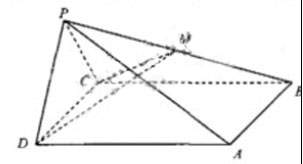 (2)求二面角
(2)求二面角 的大小
的大小
(3)求P到平面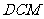 的距离
的距离
18.(本小题满分13分)
某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条
公路,汽车走公路①堵车的概率为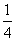 ,不堵车的概率为
,不堵车的概率为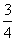 ;汽车走公路②堵车的
;汽车走公路②堵车的
概率为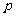 ,不堵车的概率为
,不堵车的概率为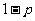 .若甲、乙两辆汽车走公路①,丙汽车由于其他
.若甲、乙两辆汽车走公路①,丙汽车由于其他
原因走公路②,且三辆车是否堵车相互之间没有影响.
(Ⅰ)若三辆汽车中恰有一辆汽车被堵的概率为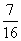 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(Ⅱ)在(1)的条件下,求三辆汽车中被堵车辆的个数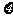 的分布列和数学期望
的分布列和数学期望
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com