
1.(2009年广东卷文)已知等比数列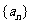 的公比为正数,且
的公比为正数,且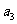 ·
·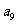 =2
=2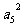 ,
,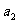 =1,则
=1,则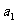 =
=
A. 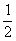 B.
B. 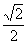 C.
C.  D.2
D.2
解析:设公比为 ,由已知得
,由已知得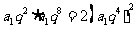 ,即
,即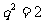 ,又因为等比数列
,又因为等比数列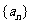 的公比为正数,所以
的公比为正数,所以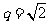 ,故
,故 ,选B
,选B
3.
若数列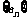 是等比数列,
是等比数列,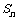 是其前n项的和,
是其前n项的和,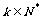 ,那么
,那么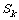 ,
,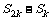 ,
,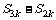 成等比数列。如下图所示:
成等比数列。如下图所示: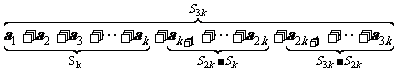
2.
对于等比数列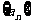 ,若
,若 ,则
,则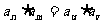 也就是:
也就是:
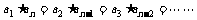 。
。
1.等比数列任意两项间的关系:如果 是等比数列的第
是等比数列的第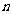 项,
项, 是等差数列的第
是等差数列的第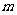 项,且
项,且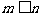 ,公比为
,公比为 ,则有
,则有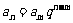
1。当n为偶数时,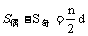 , 2。当n为奇数时,则
, 2。当n为奇数时,则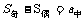 ,
,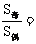
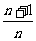 ,
,
等比数列的判定方法:
① 定义法:若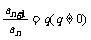 ② 等比中项:若
② 等比中项:若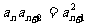 ,则数列
,则数列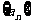 是等比数列。
是等比数列。
等比数列的通项公式:
如果等比数列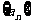 的首项是
的首项是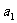 ,公比是
,公比是 ,则等比数列的通项为
,则等比数列的通项为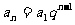 。
。
等比数列的前n项和:1。 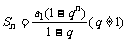 2。
2。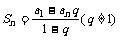 3。当
3。当 时,
时,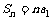
等比中项: 如果使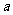 ,
,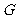 ,
,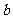 成等比数列,那么
成等比数列,那么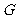 叫做
叫做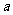 与
与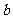 的等比中项。那么
的等比中项。那么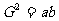 。
。
等比数列的性质:
4.设数列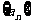 是等差数列,
是等差数列,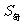 :奇数项和,
:奇数项和,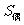 :偶数项和,
:偶数项和, 是前n项和,则有如下性质:
是前n项和,则有如下性质:
3.若数列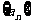 是等差数列,
是等差数列, 是其前n项的和,
是其前n项的和,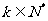 ,那么
,那么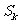 ,
,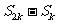 ,
, 成等差数列。如下图所示:
成等差数列。如下图所示: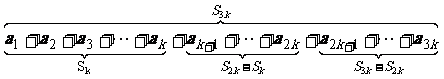
2.
对于等差数列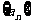 ,若
,若 ,则
,则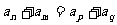 。也就是:
。也就是:
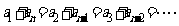 ,
,
1.等差数列任意两项间的关系:如果 是等差数列的第
是等差数列的第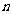 项,
项, 是等差数列的第
是等差数列的第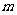 项,且
项,且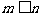 ,公差为
,公差为 ,则有
,则有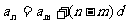
7、数列与程序框图的综合题应引起高度重视。
在近年高考中,对平面向量内容的考查的主要知识点和题型有:
等差数列的证明方法:1. 定义法:2.等差中项: 对于数列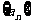 ,若
,若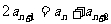
等差数列的通项公式: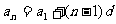 ------该公式整理后是关于n的一次函数
------该公式整理后是关于n的一次函数
等差数列的前n项和 1.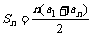 2.
2. 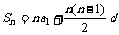 3.
3.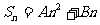
等差中项: 如果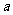 ,
,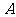 ,
,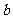 成等差数列,那么
成等差数列,那么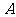 叫做
叫做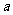 与
与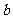 的等差中项。即:
的等差中项。即: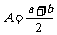 或
或
等差数列的性质:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com