
31.(2009北京理)已知数列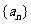 满足:
满足: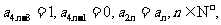 则
则 ________;
________;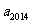 =_________.
=_________.
[答案]1,0
解析:本题主要考查周期数列等基础知识.属于创新题型. 

依题意,得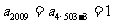 ,
, .
.
∴应填1,0.
30. (2008湖北卷15)观察下列等式:

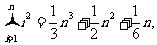
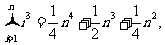
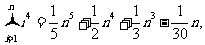
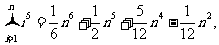
……………………………………

可以推测,当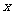 ≥2(
≥2(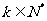 )时,
)时,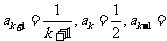

 .,0
.,0
解析:由观察可知当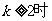 ,每一个式子的第三项的系数是成等差数列的,所以
,每一个式子的第三项的系数是成等差数列的,所以 ,
,
第四项均为零,所以 。
。
29.(2009北京文)若数列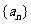 满足:
满足: ,则
,则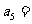 ;前8项的和
;前8项的和 .(用数字作答)
.(用数字作答)
解析:本题主要考查简单的递推数列以及数列的求和问题. 属于基础知识、基本运算的考查.
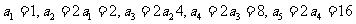 ,
,
易知 ,∴应填255.
,∴应填255.
28. (2008湖北卷14)已知函数 ,等差数列
,等差数列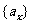 的公差为
的公差为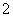 .若
.若 ,则
,则 .-6
.-6
解析:依题意 ,所以
,所以

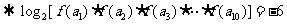
27.(2009浙江文)设等差数列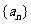 的前
的前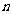 项和为
项和为 ,则
,则 ,
, ,
, ,
,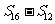 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列 的前
的前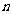 项积为
项积为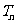 ,则
,则 ,
, ,
,
, ,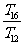 成等比数列.
成等比数列.
答案:  [命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力.
[命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力.
解析:对于等比数列,通过类比,有等比数列 的前
的前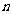 项积为
项积为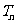 ,则
,则 ,
, ,
,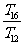 成等比数列.
成等比数列.
26.(2009浙江文)设等比数列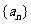 的公比
的公比 ,前
,前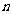 项和为
项和为 ,则
,则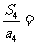 .
.
[命题意图]此题主要考查了数列中的等比数列的通项和求和公式,通过对数列知识点的考查充分体现了通项公式和前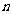 项和的知识联系.
项和的知识联系.
解析:对于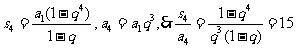
25. (2008安徽卷14)在数列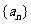 在中,
在中, ,
,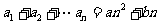 ,
, ,其中
,其中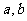 为常数,则
为常数,则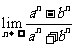 的值是
的值是
解析:1 ∵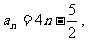 ∴
∴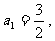 从而
从而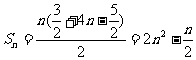 。
。
∴a=2, ,则
,则
24.(2009浙江理)设等比数列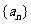 的公比
的公比 ,前
,前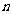 项和为
项和为 ,则
,则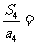 .
.
答案:15
解析:对于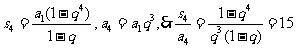
23.(2008四川卷16)设等差数列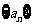 的前
的前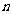 项和为
项和为 ,若
,若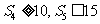 ,则
,则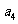 的最大值为___________。
的最大值为___________。
解析: 由题意,
由题意,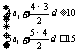 ,即
,即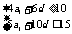 ,
, ,
,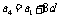 .
.
这是加了包装的线性规划,有意思.建立平面直角坐标系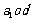 ,画出可行域
,画出可行域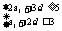 (图略),画出目标函数即直线
(图略),画出目标函数即直线 ,由图知,当直线
,由图知,当直线 过可行域内
过可行域内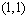 点时截距最大,此时目标函数取最大值
点时截距最大,此时目标函数取最大值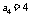 .本题明为数列,实为线性规划,着力考查了转化化归和数形结合思想.掌握线性规划问题"画-移-求-答"四步曲,理解线性规划解题程序的实质是根本.这是本题的命题意图.
.本题明为数列,实为线性规划,着力考查了转化化归和数形结合思想.掌握线性规划问题"画-移-求-答"四步曲,理解线性规划解题程序的实质是根本.这是本题的命题意图.
因约束条件只有两个,本题也可走不等式路线.设 ,
,
由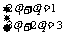 解得
解得 ,
,
∴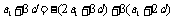 ,
,
由不等式的性质得: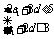
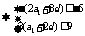


 ,即
,即
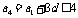 ,
, 的最大值是4.
的最大值是4.
22.(2009全国卷Ⅰ理) 设等差数列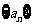 的前
的前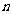 项和为
项和为 ,若
,若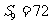 ,则
,则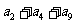 =
。
=
。
解析: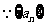 是等差数列,由
是等差数列,由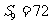 ,得
,得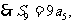

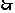
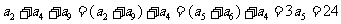 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com