
3.穿过闭合回路的磁通量φ随时间t变化的图象分别如图12-1-4①-④所示,下列关于回路中产生的感应电动势的论述,正确的是
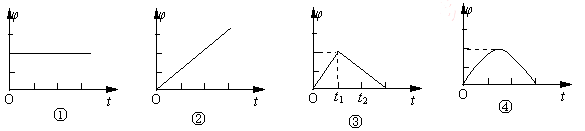
A.图①中回路产生的感应电动势恒定不变
B.图②中回路产生的感应电动势一直在变大
C.图③中回路在0-t1时间内产生的感应电动势小于在t1-t2时间内产生的感应电动势
D.图④中回路产生的感应电动势先变小再变大
2.对匝数一定的线圈,下列说法中正确的是
A.线圈放在磁场越强的位置,线圈中产生的感应电动势一定越大
B.线圈中磁通量变化越快,线圈中产生的感应电动势一定就大
C.线圈中磁通量变化越大,线圈中产生的感应电动势一定越大
D.线圈中磁通量越大,线圈中产生的感应电动势一定越大
1.对于法拉第电磁感应定律 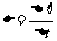 ,下面理解正确的是
,下面理解正确的是
A.穿过线圈的磁通量越大,感应电动势越大
B.穿过线圈的磁通量为零,感应电动势一定为零
C.穿过线圈的磁通量变化越大,感应电动势越大
D.穿过线圈的磁通量变化越快,感应电动势越大
24.(本题满分10分)
令 ,
,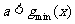 即可
即可
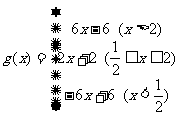 ,当
,当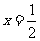 时,
时,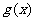 取最小值3
取最小值3
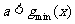 即可, 故
即可, 故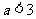 .
…………………………………10分
.
…………………………………10分
23.(本题满分10分)
(Ⅰ)直线的直角坐标方程为: ;
;
……………………3分
(Ⅱ)原点到直线的距离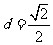 ,
,
直线参数方程为: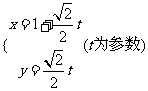 直角坐标方程为:
直角坐标方程为: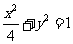 ,
,
联立得: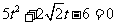 ,求得
,求得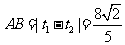
所以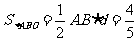 …………………………………10分
…………………………………10分
22.(本题满分10分)
(Ⅰ) 证明:

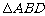 ∽
∽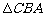
∴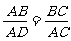 ,即
,即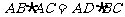 …………………………4分
…………………………4分
(Ⅱ) 由射影定理知
由射影定理知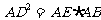
又由三角形相似可知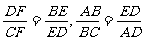 ,且
,且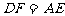
∴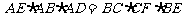 ,结合射影定理
,结合射影定理
∴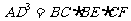 ………………
………………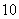 分
分
21. (本题满分12分)高.考*资+源-网
(Ⅰ)由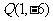 在抛物线
在抛物线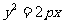 上可得,
上可得,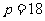 ,抛物线方程为
,抛物线方程为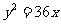 ………1分
………1分
设抛物线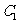 的切线方程为:
的切线方程为: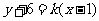
联立,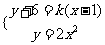 ,由
,由 ,可得
,可得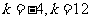
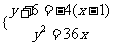 可知
可知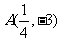
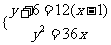 可知
可知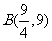 …………………………3分
…………………………3分
易求直线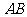 方程为
方程为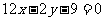 …………………………4分
…………………………4分
弦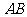 长为
长为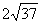 …………………………5分
…………………………5分
(Ⅱ))设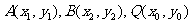 ,三个点都在抛物线
,三个点都在抛物线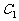 上,故有
上,故有
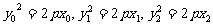 ,作差整理得
,作差整理得
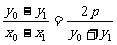 ,
,
所以直线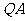 :
: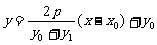 ,直线
,直线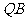 :
: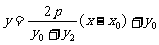
…………………………6分
因为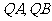 均是抛物线
均是抛物线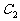 的切线,故与抛物线
的切线,故与抛物线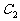 方程联立,
方程联立,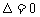 ,可得:
,可得:
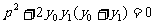 ,
,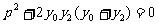
两式相减整理得: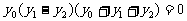 ,即可知
,即可知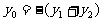 ………8分
………8分
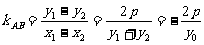
所以直线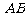 :
: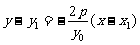 ,与抛物线
,与抛物线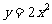 联立消去
联立消去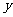
得关于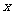 的一元二次方程:
的一元二次方程: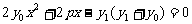 …………………………10分
…………………………10分
易知其判别式
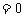 ,因而直线
,因而直线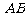 与抛物线
与抛物线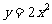 相切. ……………………12分
相切. ……………………12分
20.(本题满分12分)
解:(I)因为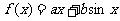 ,所以
,所以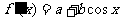 ………………1分
………………1分
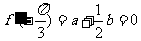 ,
,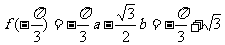
解得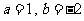 ,
………………3分
,
………………3分
此时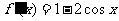 ,
,
当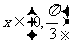 时
时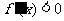 ,当
,当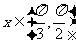 时
时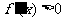 ,
,
所以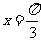 时
时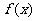 取极小值,所以
取极小值,所以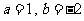 符合题目条件; ………………4分
符合题目条件; ………………4分
(II)由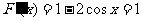 得
得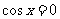 ,
,
当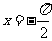 时,
时,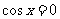 ,此时
,此时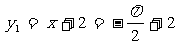 ,
,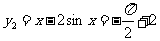 ,
,
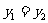 ,所以
,所以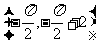 是直线
是直线 与曲线
与曲线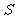 的一个切点;
的一个切点;
当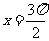 时,
时,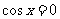 ,此时
,此时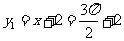 ,
,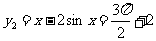 ,
,
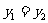 ,所以
,所以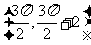 是直线
是直线 与曲线
与曲线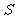 的一个切点;
的一个切点;
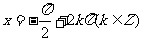 即可,无穷多组解
即可,无穷多组解
所以直线l与曲线S相切且至少有两个切点; ………………8分
对任意x∈R,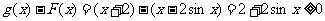 ,
,
所以 ………………11分
………………11分
因此直线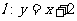 是曲线
是曲线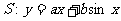 的“上夹线”. ………………12分
的“上夹线”. ………………12分
19.(本题满分12分)
解:(Ⅰ)由茎叶图可知乙班的平均水平高 ………………………………4分
(Ⅱ)甲班高于乙班平均分的共有3个人, ……………6分
从甲班10个人中任选2个人的结果总数是45 ……………8分
设从甲班这10名同学中随机抽取两名同学,求至少有一名分数高于乙班平均分记为事件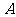 ,事件
,事件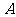 包含的结果是24,
……………10分
包含的结果是24,
……………10分
则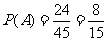 …………12分
…………12分
18.(本题满分12分)
解:(Ⅰ)连接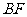 ,不妨设
,不妨设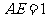 ,则
,则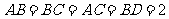 ,于是
,于是
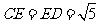 ,
,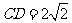 ,所以
,所以 ,
,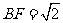 ,
, ………………… 3分
………………… 3分
所以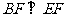 ,又
,又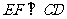 ,又
,又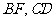 为两条相交直线
为两条相交直线
故 …………………………………………………6分
…………………………………………………6分
(Ⅱ)由(Ⅰ) ,又过
,又过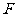 作
作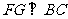 ,交
,交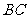 于点
于点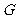 ,
,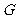 为
为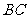 中点
中点
连接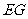 ,
,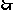
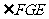 为所求二面角的平面角
…………………………9分
为所求二面角的平面角
…………………………9分
所以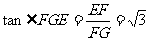 ,
, 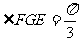 ……………………12分
……………………12分
高.考*资+源-网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com