
16.(14分)
⑴ 从A点射出的粒子,由A到A′的运动时间为T,根据运动轨迹和对称性可得
x轴方向 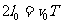 (1分)
(1分)
y轴方向
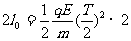 (1分)
(1分)
得: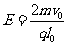 (2分)
(2分)
⑵ 设到C点距离为△y处射出的粒子通过电场后也沿x轴正方向,粒子第一次达x轴用时△t,水平位移为△x,则 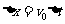
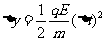 (1分)
(1分)
若满足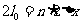 ,则从电场射出时的速度方向也将沿x轴正方向 (2分)
,则从电场射出时的速度方向也将沿x轴正方向 (2分)
解之得: (2分)
(2分)
即AC间y坐标为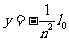 (n = 1,2,3,……) (1分)
(n = 1,2,3,……) (1分)
⑶ 当n=1时,粒子射出的坐标为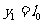
当n=2时,粒子射出的坐标为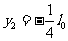
当n≥3时,沿x轴正方向射出的粒子分布在y1到y2之间(如图)y1到y2之间的距离为
L= y1-y2=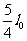 则磁场的最小半径为
则磁场的最小半径为 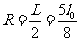 (2分)
(2分)
若使粒子经磁场偏转后汇聚于一点,粒子的运动半径与磁场圆的半径相等(如图),(轨迹圆与磁场圆相交,四边形PO1QO2为棱形) 由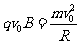 得:
得: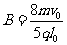 (2分)
(2分)

36、如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向。在电场左边界上A (-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子。从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场。若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图。不计粒子的重力及它们间的相互作用。
(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子。从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场。若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图。不计粒子的重力及它们间的相互作用。
⑴求匀强电场的电场强度E;
⑵求在AC间还有哪些位置的粒子,通过电场后也能沿x轴正方向运动?
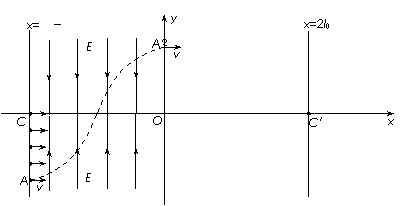 ⑶若以直线x=2l0上的某点为圆心的圆形区域内,分布着垂直于xOy平面向里的匀强磁场,使沿x轴正方向射出电场的粒子,经磁场偏转后,都能通过直线x=2l0与圆形磁场边界的一个交点处,而便于被收集,则磁场区域的最小半径是多大?相应的磁感应强度B是多大?
⑶若以直线x=2l0上的某点为圆心的圆形区域内,分布着垂直于xOy平面向里的匀强磁场,使沿x轴正方向射出电场的粒子,经磁场偏转后,都能通过直线x=2l0与圆形磁场边界的一个交点处,而便于被收集,则磁场区域的最小半径是多大?相应的磁感应强度B是多大?
35、 如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B。折线的顶角∠A=90°,P、Q是折线上的两点, AP=AQ=L。现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力。
如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B。折线的顶角∠A=90°,P、Q是折线上的两点, AP=AQ=L。现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力。
(1)若P、Q间外加一与磁场方向垂直的匀强电场,能使速度为v0射出的微粒沿PQ直线运动到Q点,则场强为多大?
(2)撤去电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,求初速度v应满足什么条件?
(3)求第(2)中微粒从P点到达Q点所用的时间。
⑴由电场力与洛伦兹力平衡得:qE=qv0B
得:E=v0B(3分)
⑵根据运动的对称性,微粒能从P点到达Q点,应满足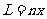 (2分)
(2分)
其中x为每次偏转圆弧对应的弦长,偏转圆弧对应的圆心角为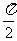 或
或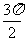 。
。
 设圆弧的半径为R,则有2R2=x2,可得:
设圆弧的半径为R,则有2R2=x2,可得: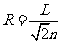 (1分)
(1分)
又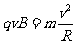
由①②③式得: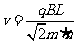 ,n=1、2、3、……(3分)
,n=1、2、3、……(3分)
⑶当n取奇数时,微粒从P到Q过程中圆心角的总和为
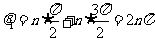 ,
,
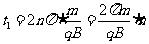 ,其中n=1、3、5、……(2分)
,其中n=1、3、5、……(2分)
当n取偶数时,微粒从P到Q过程中圆心角的总和为

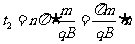 ,其中n=2、4、6、……(2分)
,其中n=2、4、6、……(2分)
34、如图所示,在y轴的右方有一磁感应强度为B的方向垂直纸面向外的匀强磁场,在x轴的下方有一场强为E的方向平行x轴向右的匀强电场。有一铅板放置在y轴处,且与纸面垂直。现有一质量为m、电荷量为q的粒子由静止经过加速电压为U的电场加速,然后以垂直于铅板的方向从A处沿直线穿过铅板,而后从x轴上的D处以与x轴正向夹角为60°的方向进入电场和磁场叠加的区域,最后到达y轴上的C点。已知OD长为l,求:
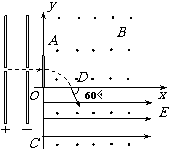 (1)粒子经过铅板时损失了多少动能?
(1)粒子经过铅板时损失了多少动能?
(2)粒子到达C点时的速度多大?
(1)
由动能定理可知此带电粒子穿过铅板前的动能 ,--1分
,--1分
根据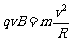 ,得
,得 ,--2分
,--2分
又由几何知识可得(如图)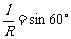
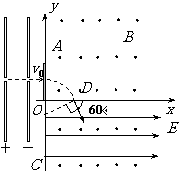 即
即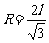 ,--1分 故
,--1分 故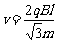 。--1分
。--1分
由于洛伦兹力不做功,带电粒子穿过铅板后的动能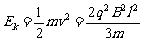 ,--1分
,--1分
因此粒子穿过铅板后动能的损失为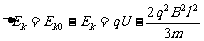 --1分
--1分
(2)从D到C只有电场力对粒子做功,电场力做功与路径无关,根据动能定理,有
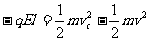 ,--3分
,--3分
解得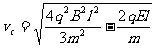 --3分
--3分
33、如图所示,粒子源S可以不断地产生质量为m、电荷量为+q的粒子(重力不计).粒子从O1孔漂进(初速不计)一个水平方向的加速电场,再经小孔O2进入相互正交的匀强电场和匀强磁场区域,电场强度大小为E,磁感应强度大小为B1,方向如图.虚线PQ、MN之间存在着水平向右的匀强磁场,磁感应强度大小为B2(图中未画出).有一块折成直角的硬质塑料板abc(不带电,宽度很窄,厚度不计)放置在PQ、MN之间(截面图如图),a、c两点恰在分别位于PQ、MN上,ab=bc=L,α= 45°.现使粒子能沿图中虚线O2O3进入PQ、MN之间的区域.
(1) 求加速电压U1.
(2) 假设粒子与硬质塑料板相碰后,速度大小不变,方向变化遵守光的反射定律.粒子在PQ、MN之间的区域中运动的时间和路程分别是多少?


(1)粒子源发出的粒子,进入加速电场被加速,速度为v0,根据能的转化和守恒定律得: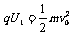 (2分)
(2分)
要使粒子能沿图中虚线O2O3进入PQ、MN之间的区域,则粒子所受到向上的洛伦兹力与向下的电场力大小相等,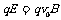 得到
得到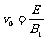 (2分)
(2分)
将②式代入①式,得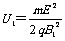 (1分)
(1分)
(2)粒子从O3以速度v0进入PQ、MN之间的区域,先做匀速直线运动,打到ab板上,以大小为v0的速度垂直于磁场方向运动.粒子将以半径R在垂直于磁场的平面内作匀速圆周运动,转动一周后打到ab板的下部.由于不计板的厚度,所以质子从第一次打到ab板到第二次打到ab板后运动的时间为粒子在磁场运动一周的时间,即一个周期T.
由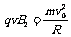 和运动学公式
和运动学公式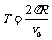 ,得
,得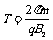 (2分)
(2分)
粒子在磁场中共碰到2块板,做圆周运动所需的时间为 (2分)
(2分)
粒子进入磁场中,在v0方向的总位移s=2Lsin45°,时间为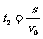 (2分)
(2分)
则t=t1+t2=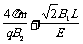 (2分)
(2分)
32、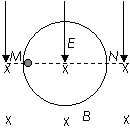 如图所示,有位于竖直平面上的半径为R的圆形光滑绝缘轨道,其上半部分处于竖直向下、场强为E的匀强电场中,下半部分处于水平向里的匀强磁场中;质量为m,带正电为q的小球,从轨道的水平直径的M端由静止释放,若小球在某一次通过最低点时对轨道的压力为零,求:
如图所示,有位于竖直平面上的半径为R的圆形光滑绝缘轨道,其上半部分处于竖直向下、场强为E的匀强电场中,下半部分处于水平向里的匀强磁场中;质量为m,带正电为q的小球,从轨道的水平直径的M端由静止释放,若小球在某一次通过最低点时对轨道的压力为零,求:
(1)磁感强度B的大小。
(2)小球对轨道最低点的最大压力。
(3)若要小球在圆形轨道内作完整的圆周运动,小球从轨道的水平直径的M端下滑的最小速度。
解:(1)小球在轨道上来回运动时受重力、支持力、洛伦兹力,但只 有重力做功,因此小球的机械能守恒。从M到最低点有
有重力做功,因此小球的机械能守恒。从M到最低点有 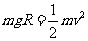 在最低点有
在最低点有
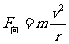 即
即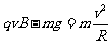 联解(1)(2)得
联解(1)(2)得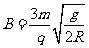
(2)小球从M到N以及在轨道上来回运动时受重力、支持力、洛伦兹力,但总只有重力做功,因此小球的机械能始终守恒。从N到最低点时对轨道最低点的有最大压力。
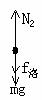 在最低点有
在最低点有
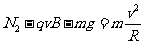 联解(1)(3)得N2=6mg
联解(1)(3)得N2=6mg
(3)要小球在圆形轨道内作完整的圆周运动,此时对圆形轨道的最高点压力为零,
设小球从轨道的水平直径的M端下滑的最小速度为v0,在最高点速度为v1。
从M→轨道的最高点,据动能定理:
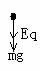
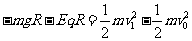 在圆形轨道的最高点:
在圆形轨道的最高点:
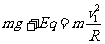 联解(4)(5)得
联解(4)(5)得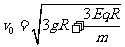
20、(14分)设集合W由满足下列两个条件的数列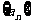 构成:
构成:
①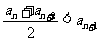 ;②存在实数M,使
;②存在实数M,使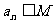 。(n为正整数)
。(n为正整数)
(Ⅰ)在只有5项的有限数列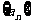 、
、 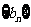 中,其中
中,其中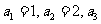 =3,
=3,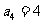 ,
,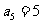 ;
;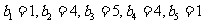 ;试判断数列
;试判断数列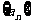 、
、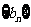 是否为集合W中的元素;
是否为集合W中的元素;
(Ⅱ)设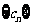 是各项为正数的等比数列,
是各项为正数的等比数列,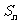 是其前
是其前 项和,
项和,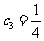 ,
,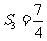 ,试证明
,试证明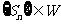 ,并写出
,并写出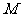 的取值范围;
的取值范围;
(Ⅲ)设数列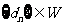 ,对于满足条件的M的最小值M0,都有
,对于满足条件的M的最小值M0,都有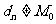 (
(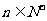 )。
)。
求证:数列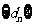 单调递增。
单调递增。
19、(13分)在直角坐标系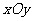 中,点
中,点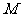 到F1
到F1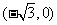 、F2
、F2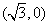 的距离之和是4,点
的距离之和是4,点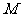 的轨迹
的轨迹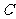 与
与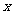 轴的负半轴交于点
轴的负半轴交于点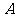 ,不过点
,不过点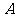 的直线
的直线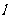 :
: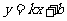 与轨迹
与轨迹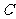 交于不同的两点
交于不同的两点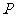 和
和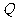 .
.
(1)求轨迹 的方程;
的方程;
(2)当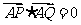 时,求
时,求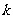 与
与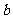 的关系,并证明直线
的关系,并证明直线 过定点.
过定点.
18、(13分)已知函数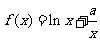 。
。
(Ⅰ)当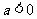 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在[1,e]上的最小值是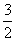 ,求
,求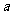 的值.
的值.
17、(14分)某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响。已知师父加工一个零件是精品的概率为 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为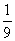 。
。
(Ⅰ)求徒弟加工2个零件都是精品的概率;
(Ⅱ)求徒弟加工该零件的精品数多于师父的概率;
(Ⅲ)设师徒二人加工出的4个零件中精品个数为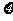 ,求
,求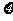 的分布列与均值
的分布列与均值 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com