
4.一个几何体的三视图如图所示,那么此几何体的侧面积(单位:㎝2)为 ( )
 A.80 B.60
A.80 B.60
C.40 D.20
3.已知平面向量 ,
, 的值为 ( )
的值为 ( )
A.1 B.-1
C.4 D.-4
2.已知命题 ,那么命题
,那么命题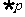 为 ( )
为 ( )
A. B.
B.
C. D.
D.
1.复数 等于 ( )
等于 ( )
A. B.
B. C.
C. D.
D.
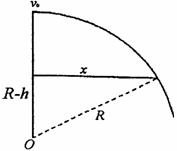
42、一个质量为m带电量为+q的小球以水平初速度v0自离地面h 高度处做平抛运动。不计空气阻力。重力加速度为g。试回答下列问题:
高度处做平抛运动。不计空气阻力。重力加速度为g。试回答下列问题:
(1)小球自抛出到第一次落地至点P的过程中发生的位移s大小是多少?
(2)若在空间加一个竖直方向的匀强电场,发现小球水平抛出后做匀速直线运动,则匀强电场强度E是多大?
(3)若在空间再加一个垂直纸面向外的匀强磁场,发现小球第一次落地点仍然是P。试问磁感应强度B是多大?

解:(1)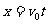 (1分)
(1分) 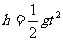 (1分)
(1分)
得  (2分)
(2分)
 (2)mg=qE
(2)mg=qE  (2分)
(2分)
(3)由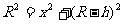 (1分)
(1分)
得  (2分)
(2分)
 (2分)
(2分)
∴
 (2分)
(2分)
41、如图所示,两个同心圆,半径分别为r和2r,在两圆之间的环形区域内存在垂直纸面向里的匀强磁场,磁感应强度为B。圆心O处有一放射源,放出粒子的质量为m,带电量为q,假设粒子速度方向都和纸面平行。
(1)图中箭头表示某一粒子初速度的方向,OA与初速度方向夹角为60°,要想使该粒子经过磁场第一次通过A点,则初速度的大小是多少?
(2)要使粒子不穿出环形区域,则粒子的初速度不能超过多少?
1)如图所示,设粒子在磁场中的轨道半径为R1,则由几何关系得
 R1=
R1=  (2分)
(2分)
由q 1B=m
1B=m (2分)
(2分)
得 1=
1= (2分)
(2分)
(2)设粒子在磁场中的轨道半径为R2,
则由几何关系(2r- R2)2= R22+ r2 (1分)
得R2=3r/4 (1分)
由q 2B=m
2B=m (2分)
(2分)
得 2=
2= (1分)
(1分)
40、 如图所示,ABCDEF是一边长为工的正六边形盒,各边均为绝缘板,盒外有方向垂直纸面向里、范围足够大的匀强磁场,磁感应强度大小为B.在盒内有两个与AF边平行的金属板M、N,且金属板N靠近盒子的中心O点,金属板M和盒子AF边的中点均开有小孔,两小孔与O点在同一直线上.现在O点静止放置一质量为m、电荷量为q的带正电粒子(不计粒子的重力).
如图所示,ABCDEF是一边长为工的正六边形盒,各边均为绝缘板,盒外有方向垂直纸面向里、范围足够大的匀强磁场,磁感应强度大小为B.在盒内有两个与AF边平行的金属板M、N,且金属板N靠近盒子的中心O点,金属板M和盒子AF边的中点均开有小孔,两小孔与O点在同一直线上.现在O点静止放置一质量为m、电荷量为q的带正电粒子(不计粒子的重力).
(1)如果在金属板N、M间加上电压UNM=U0时,粒子从AF边小孔射出后直接打在A点,试求电压Uo的大小.
(2)如果改变金属板N、M间所加电压,试判断粒子从AF边小孔射出后能否直接打在C 点.若不能,说明理由;若能,请求出此时电压UNM的大小.
(3)如果给金属板N、M间加一合适的电压,粒子从AF边小孔射出后恰好能以最短时间回到该小孔(粒子打在盒子各边时都不损失动能),试求最短时间.
(1) 依题意,R=L/4
由qvB=mv2/R
qU0=
得U0=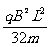
(2)设AF中点为G,连接GC,作其垂直平分线,与AF延长线交点即为圆心
由相似三角形得R’=O’G=13L/4
qvB=mv2/R’
q=
∴UNM=
(3)由于粒子在磁场中运动周期T= ,T与速率无关
,T与速率无关
粒子撞击BC中点和DE中点后回到G,用时最短
圆周半径R”=3L/2
 得到最短时间t=
得到最短时间t= =
=
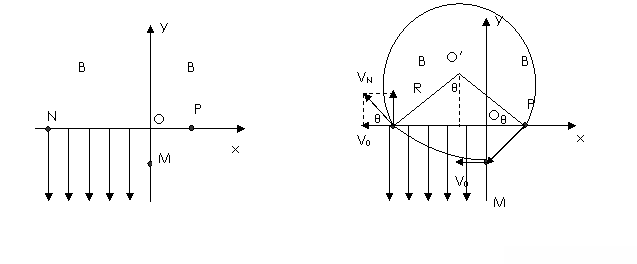
39、 如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场;第四象限无电场和磁场。现有一质量为m、电荷量为q的粒子以
如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场;第四象限无电场和磁场。现有一质量为m、电荷量为q的粒子以 速度v0从y轴上的M点沿x轴负方向进入电场,不计粒子的重力,粒子经x轴上的N点和P点最后又回到M点,设OM=L,ON=2L.求:
速度v0从y轴上的M点沿x轴负方向进入电场,不计粒子的重力,粒子经x轴上的N点和P点最后又回到M点,设OM=L,ON=2L.求:
(1)带电粒子的电性,电场强度E的大小;
(2)带电粒子到达N点时的速度大小和方向;
(3)匀强磁场的磁感应强度的大小和方向;
(4)粒子从M点进入电场,经N、P点最后又回到M点所用的时间。
[解析](1)粒子从M至N运动过程有: 1
1
加速度 2
2
 运动时间
运动时间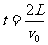 3
3
由123得电场强度 则
则 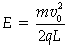 4
4
(2)设vN与x成θ角
带电粒子到N点速度

 5
5
(3)带电粒子在磁场中做圆周运动的轨迹如图所示,圆心在O′处,设半径为R,由几何关系知带电粒子过P点的速度方向与x成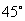 角,则OP=OM=L
角,则OP=OM=L
则 6
6
由牛顿第二定律得: 7
7
由67解得:
(4)粒子从M至N时间: 8
8
粒子在磁场中运动时间: 9
9
粒子从P至M运动时间 10
10
从M点进入电场,经N、P回M所用时间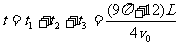
38、某同学设想用带电粒子的运动轨迹做出“0”、“8”字样,首先,如图甲所示,在真空空间的竖直平面内建立 坐标系,在
坐标系,在 和
和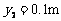 处有两个与
处有两个与 轴平行的水平界面
轴平行的水平界面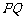 和
和 把空间分
把空间分 成Ⅰ、Ⅱ、Ⅲ三个区域,在三个区域中分别存在匀强磁场
成Ⅰ、Ⅱ、Ⅲ三个区域,在三个区域中分别存在匀强磁场 、
、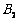 、
、 ,其大小满足
,其大小满足 ,方向如图甲所示.在Ⅱ区域中的
,方向如图甲所示.在Ⅱ区域中的 轴左右两侧还分别存在匀强电场
轴左右两侧还分别存在匀强电场 、
、 (图中未画出),忽略所有电、磁场的边缘效应.
(图中未画出),忽略所有电、磁场的边缘效应. 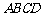 是以坐标原点
是以坐标原点 为中心对称的正方形,其边长
为中心对称的正方形,其边长 .现在界面
.现在界面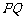 上的
上的 处沿
处沿 轴正方向发射一比荷
轴正方向发射一比荷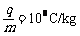 的带正电荷的粒子(其重力不计),粒子恰能沿图中实线途经
的带正电荷的粒子(其重力不计),粒子恰能沿图中实线途经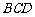 三点后回到
三点后回到 点并做周期性运动,轨迹构成一个“0”字.己知粒子每次穿越Ⅱ区域时均做直线运动.
点并做周期性运动,轨迹构成一个“0”字.己知粒子每次穿越Ⅱ区域时均做直线运动.
(1)求 、
、 场的大小和方向.
场的大小和方向.
 (2)去掉Ⅱ和Ⅲ区域中的匀强电场和磁场,其他条件不变,仍在
(2)去掉Ⅱ和Ⅲ区域中的匀强电场和磁场,其他条件不变,仍在 处以相同的速度发射相同的粒子,请在Ⅱ和Ⅲ区城内重新设计适当的匀强电场或匀强磁场,使粒子运动的轨迹成为上、下对称的“8”字,且粒子运动的周期跟甲图中相同,请通过必要的计算和分析,求出你所设计的“场”的大小、方向和区域,并在乙图中描绘出带电粒子的运动轨迹和你所设计的“场”.(上面半圆轨迹己在图中画出)
处以相同的速度发射相同的粒子,请在Ⅱ和Ⅲ区城内重新设计适当的匀强电场或匀强磁场,使粒子运动的轨迹成为上、下对称的“8”字,且粒子运动的周期跟甲图中相同,请通过必要的计算和分析,求出你所设计的“场”的大小、方向和区域,并在乙图中描绘出带电粒子的运动轨迹和你所设计的“场”.(上面半圆轨迹己在图中画出)

37、如图(a)所示,在真空中,半径为b的虚线所围的圆形区域内存在匀强磁场,磁场方向与纸面垂直.在磁场右侧有一对平行金属板M和N,两板间距离也为b,板长为2b,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上.
有一电荷量为+q、质量为m的带电粒子,以速率v0从圆周上的P点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如图(b)所示电压u.最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力.
(1)求磁场的磁感应强度B;
(2)求交变电压的周期T和电压U0的值;
 (3)若t = 时,将该粒子从MN板右侧沿板的中心线O2O1,仍以速率v0射入M、N之间,求粒子从磁场中射出的点到P点的距离.
(3)若t = 时,将该粒子从MN板右侧沿板的中心线O2O1,仍以速率v0射入M、N之间,求粒子从磁场中射出的点到P点的距离.
(1)粒子自P点进入磁场,从O1点水平飞出磁场,运动的半径必为b,………(1分)
 …………………………(1分)
…………………………(1分)
解得  ………………………………………(1分)
………………………………………(1分)
由左手定则可知,磁场方向垂直纸面向外…………………(1分)
(2)粒子自O1点进入电场,最后恰好从N板的边缘平行飞出,设运动时间为t,则
2b = v0t …………………………………………………(1分)
 …………………(1分)
…………………(1分)
t = nT(n=1,2,…) ………………………………(1分)
解得  (n=1,2,…) …………………(1分)
(n=1,2,…) …………………(1分)
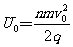 (n=1,2,…) ……………………………(1分)
(n=1,2,…) ……………………………(1分)
 (3)当t = 粒子以速度v0沿O2O1射入电场时,则该粒子恰好从M板边缘以平行于极板的速度射入磁场,且进入磁场的速度仍为v0,运动的轨道半径仍为b.…(2分)
(3)当t = 粒子以速度v0沿O2O1射入电场时,则该粒子恰好从M板边缘以平行于极板的速度射入磁场,且进入磁场的速度仍为v0,运动的轨道半径仍为b.…(2分)
设进入磁场的点为Q,离开磁场的点为R,圆心为O3,如图所示,四边形OQ O3R是菱形,故O R∥ QO3.……………………(2分)
所以P、O、R三点共线,即POR为圆的直径.即PR间的距离为2b.………(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com