8．特殊模型法

例19 　已知m,n是直线，α、β、γ是平面，给出下列命题：

①若α⊥γ，β⊥γ，则α∥β；

②若n⊥α，n⊥β，则α∥β；

③若α内不共线的三点到β的距离都相等，则α∥β；

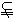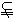④若nα，mα，且n∥β,m∥β，则α∥β；

⑤若m,n为异面直线，n∈α，n∥β，m∈β,m∥α,则α∥β；

则其中正确的命题是　　　　　　　　　　　　 。(把你认为正确的命题序号都填上)

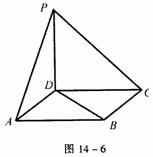
解 　依题意可构造正方体AC₁，如图14-5，在正方体中逐一判断各命题易得正确命题的是②⑤。

7．特殊方程法

例18 　直线l过抛物线y²=a(x+1)(a>0)的焦点，并且与x轴垂直，若l被抛物线截得的线段长为4，则a=　　　　　　　　　　　　 。

解 　∵抛物线y²=a(x+1)与抛物线y²=ax具有相同的垂直于对称轴的焦点弦长，故可用标准方程y²=ax替换一般方程y²=a(x+1)求解，而a值不变。由通径长公式得a=4。

6．特殊点法

例17 　椭圆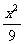+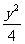=1的焦点为F₁、F₂，点P为其上的动点，当∠F₁PF₂为钝角时，点P横坐标的取值范围是　　　　　　 　　　　　 。

解 　设P(x,y)，则当∠F₁PF₂=90°时，点P的轨迹方程为x²+y²=5，由此可得点P的横坐标x=±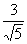，又当点P在x轴上时，∠F₁PF₂=0；点P在y轴上时，∠F₁PF₂为钝角，由此可得点P横坐标的取值范围是-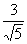<x<。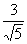

5．图形特殊位置法

例16 　已知SA，SB，SC两两所成角均为60°，则平面SAB与平面SAC所成的二面角为　　　　　　　　　　　　 。

解 　取SA=SB=SC，将问题置于正四面体中研究，不难得平面SAB与平面SAC所成的二面角为arccos。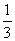

3．特殊角法

例14 　cos²α+cos²(α+120°)+cos²(α+240°)的值为　　　　　　　　 　　　　　　　 。

解　 本题的隐含条件是式子的值为定值，即与α无关，故可令α=0°，计算得上式值为。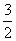

例15 　已知等差数列{a_n}的公差d≠0，且a₁,a₃,a₉成等比数列，则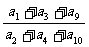的值是　　　　　　　　　　 。

解　 考虑到a₁,a₃,a₉的下标成等比数列，故可令a_n=n，又易知它满足题设条件，于是=。

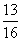2．特殊函数法

例13　 如果函数f(x)=x²+bx+c对任意实数t都有f(2+t)=f(2-t)，那么f(1),f(2),f(4)的大小关系是　　　　　　　　　　　　 。

解 　由于f(2+t)=f(2-t)，故知f(x)的对称轴是x=2。可取特殊函数f(x)=(x-2)²,即可求得f(1)=1,f(2)=0,f(4)=4。∴f(2)<f(1)<f(4)。

1.特殊值法

例12 　设a>b>1，则log_ab,log_ba,log_abb的大小关系是　　　　　　　　　　　　　 。

解 　考虑到三个数的大小关系是确定的，不妨令a=4,b=2，则log_ab=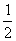,log_ba=2,log_abb=,

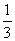∴log_abb<log_ab<log_ba。

例9 　若关于x的方程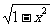=k(x-2)有两个不等实根，则实数k的取值范围是　　　　　　　　　　　　　 。

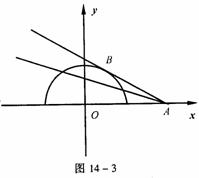
解 　令y₁=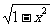,y₂=k(x-2),由图14-3可知k_AB<k≤0，其中AB为半圆的切线，计算得k_AB= -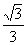,∴-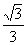<k≤0。

例10 　已知两点M(0,1),N(10,1) ，给出下列直线方程

①5x-3y-22=0;②5x-3y-52=0;③x-y-4=0;④4x-y-14=0。在直线上存在点P满足|MP|=|NP|+6的所有直线方程的序号是 　　　　　　 。

解　 由|MP|=|NP|+6可知，点P的轨迹是以M(0，1)，N(10，1)为焦点，实轴长为6的双曲线的右支，其方程为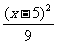-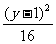=1，(x>5)。本题实质上可转化为考察所给直线与双曲线的右支有无交点的问题，结合图形判断，易得②③直线与双曲线的右支有交点。

例11 　点P(x,y)是曲线C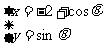：(θ为参数，0≤θ<π)上任意一点，则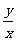的取值范围是　　　　　　　　　　　 。

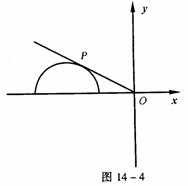
解 　曲线C的普通方程为(x+2) ² +y²=1(y≥0)，则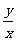可视为P点与原点O连线的斜率，结合图形14-4判断易得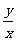的取值范围是[-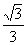，0]。

例1 　已知数列{a_n}、{b_n}都是等差数列，a₁=0、b₁= -4，用S_k、S′_k、分别表示数列{a_n}、{b_n}的前k项和(k是正整数)，若S_k+S′_k =0，则a_k+b_k的值为　　　　　　　　　　　 。

解　 法一 　直接应用等差数列求和公式S_k=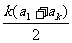，得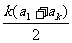+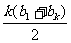=0，又a₁+b₁= -4, ∴a_k+b_k=4。

法二 　由题意可取k=2(注意：k≠1，为什么？)，于是有a₁+a₂+b₁+b₂=0，因而a₂+b₂=4,即a_k+b_k=4。

例2 　乒乓球队的10名队员中有3名主力队员，派5名参加比赛。3名主力队员要安排在第一、三、五位置，其余7名队员选2名安排在第二、四位置，那么不同的出场安排共有种(用数字作答)。

解 　三名主力队员的排法有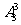种，其余7名队员选2名安排在第二、四位置上有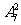种排法，故共有排法数A₃³A₇²=252种。

例3 　如图14-1，E、F分别为正方体的面ADD₁A₁、面BCC₁B₁的中心，则四边形BFD₁E在该正方体的面上的射影可能是　 　　　　　 (要求：把可能的图的序号都填上)。

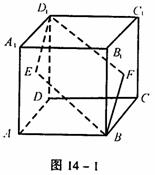
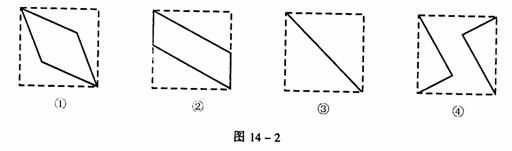
解 　正方体共有3 组对面，分别考察如下：(1)四边形BFD₁E在左右一组面上的射影是图③。因为B点、F点在面AD₁上的射影分别是A点、E点。(2)四边形BFD₁E在上下及前后两组面上的射影是图②。因为D₁点、E点、F点在面AC上的射影分别是D点、AD的中点、BC的中点；B点、E点、F点在面DC₁上的射影分别是C点、DD₁的中点、CC₁的中点。故本题答案为②③。

例4 　已知抛物线的焦点坐标为F(2,1)，准线方程为2x+y=0，则其顶点坐标为　　　　　　　　　　　　　　　　　 。

解 　过焦点F(2,1)作准线的垂线段，由解几知识可得抛物线顶点为垂线段的中点。又由于准线的斜率k= -2,k_OF=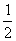，∴O为垂足，从而易得OF的中点，即顶点为(1, )。

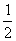例5 　老师给出一个函数y=f(x)，四个学生甲、乙、丙、丁各指出这个函数的一个性质：

甲：对于x∈R，都有f(1+x)=f(1-x)　　　　　　　　 乙：在 (-∞,0上函数递减

丙：在(0,+∞)上函数递增　　　　　　　　　　　　　　　 丁：f(0)不是函数的最小值

如果其中恰有三人说得正确，请写出一个这样的函数　　　　　　　　　 。

解 　由题意知，以甲、乙、丙、丁四个条件中任意三个为一组条件，写出符合条件的一个函数即可。例如同时具备条件甲、乙、丁的一个函数为y=(x-1)²。

例6 　若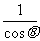-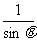=1，则sin2θ的值等于　　　　　　　　　　　 。

解 　由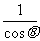-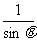=1得sinθ-cosθ=sinθcosθ　 ①

令sin2θ=t，则①式两边平方整理得t²+4t-4=0，解之得t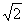=2-2。

例7 　已知z₁=3+4i,z₂= -2-5i,则arg()=　　　　　　　　　　　 。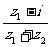

解 　将z₁=3+4i,z₂= -2-5i代入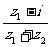整理得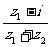=3i，故arg()=。

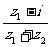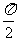例8　 若(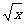+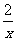)ⁿ展开式中的第5项为常数，则n=　　　　　　　　　 。

解　 由T_r+1=C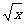_n^r()^n-r(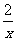)^r=C_n^r2^rx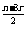及题意可知，当r=4时，n-3r=0，∴n=12。

同选择题一样，填空题也属小题，其解题的基本原则是“小题不能大做”。解题的基本策略是：巧做。解题的基本方法一般有：直接求解法，图像法和特殊化法(特殊值法，特殊函数法，特殊角法，特殊数列法，图形特殊位置法，特殊点法，特殊方程法，特殊模型法)等。

[例题解析]