
2.某邮局只有0.60元,0.80元,1.10元的三种邮票。现有邮资为7.50元的邮件一件,为使粘贴邮票的张数最少,且资费恰为7.50元,则最少要购买邮票( )
A.7张 B.8张 C.9张 D.10张
1.已知直线l⊥平面α,直线m 平面β,有下面四个命题,其中正确命题是( )
平面β,有下面四个命题,其中正确命题是( )
①α∥β l⊥m ②α⊥β
l⊥m ②α⊥β l∥m ③l∥m
l∥m ③l∥m α⊥β ④l⊥m
α⊥β ④l⊥m α∥β
α∥β
A.①与② B.①与③ C.②与④ D.③与④
问题的条件不完备,结论不确定是探索性问题的基本特征,从探索性问题的解题过程来看,没有确定的模式,可变性多,对观察、试验、联想、类比、猜想、抽象、概括,特别是对发现问题、分析问题的能力要求较高,探索性问题的解题策略有:
1攻略之一--特殊值探路,一般化证明
从最简单、最特殊的情况出发,有时也可借助直觉观察或判断,推测出命题的结论,必要时给出严格证明。
[例1]已知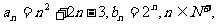 试判断
试判断 与
与 的大小关系。
的大小关系。
解析:由 <
< ,
, >
> ,
, >
> ,
, >
> ,
, ,
, <
< ,
, <
< ……猜想出结论:当
……猜想出结论:当 时,
时, ;当
;当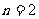 、3、4时
、3、4时 >
> ,当
,当 或
或 时
时 <
< ,然后用数学归纳法证明猜想的正确性。
,然后用数学归纳法证明猜想的正确性。
2攻略之二--假设存在,推理检验
此类题型需从题目所给出的条件及所探求的结论两方面入手,充分挖掘题设条件的内涵与外延,积极向所探究的结论靠拢。解答这类问题的一般思路是:先假定对象存在,运用条件进行推理。若得到相应的合理结论,断言这个对象是存在的;若出现矛盾,则否定先前假设,断言对象是不存在的。
[例2]抛物线过定点A(0,2)且以x轴为准线。
(1)求抛物线的顶点M的轨迹C。
(2)问过定点B ,1
,1 是否存在一对互相垂直的直线同时都与轨迹C有公共点?证明你的结论。
是否存在一对互相垂直的直线同时都与轨迹C有公共点?证明你的结论。
解析:(1)利用数形结合法,根据抛物线定义可求得动点M的轨迹方程为:
x +4(y-1)
+4(y-1) = 4(y≠0)
= 4(y≠0)
(2)过点B的直线与曲线C有交点需满足什么条件?两直线垂直的条件又是什么?这两者中有何关系?从而推出合理的结论。
设过点B ,1
,1 的直线L为:y-1=k(x+
的直线L为:y-1=k(x+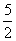 ),L与C有交点的条件为方程组
),L与C有交点的条件为方程组 有解
有解
现假设存在一对过B且与轨迹C有公共点的互相垂直的直线L 和L
和L ,则有
,则有 ,但由上述结果知
,但由上述结果知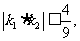 这就产生矛盾,故这样的直线不存在。
这就产生矛盾,故这样的直线不存在。
[例3](2008年湖北高考试题)已知数列 和
和 满足:
满足: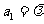 ,
, 其中
其中 为实数,
为实数, 为正整数。
为正整数。
(Ⅰ)对任意实数 ,证明数列
,证明数列 不是等比数列;
不是等比数列;
(Ⅱ)试判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)设 ,
, 为数列
为数列 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有
 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
 矛盾。
矛盾。
所以{an}不是等比数列。
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1( an-2n+14)
an-2n+14)
= (-1)n·(an-3n+21)=-
(-1)n·(an-3n+21)=- bn
bn
又b1=-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18)
≠0,由上可知bn≠0,∴ (n∈N+).
(n∈N+).
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,- 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)·(- )n-1,于是可得
)n-1,于是可得
Sn=-
要使a<Sn<b对任意正整数n成立,
即a<-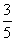 (λ+18)·[1-(-
(λ+18)·[1-(- )n]〈b(n∈N+)
)n]〈b(n∈N+)
 ①
①
当n为正奇数时,1<f(n)
∴f(n)的最大值为f(1)= ,f(n)的最小值为f(2)=
,f(n)的最小值为f(2)=  ,
,
于是,由①式得 a<-
a<-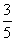 (λ+18),<
(λ+18),<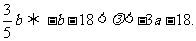
当a<b 3a时,由-b-18
3a时,由-b-18 =-3a-18,不存在实数满足题目要求;
=-3a-18,不存在实数满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18)
点评:本小题主要考查等比数列的定义、数列求和、不等式等基础知识和分类讨论的思想,考查综合分析问题的能力和推理认证能力。对于参数存在型探索性命题,其求解关键是对参数进行合理全面地分类讨论。这类探索性命题结论的成立与否取决于参数的范围的取舍。
3攻略之三--等价转化,探求条件
使用等价转化思想,找出命题成立的充要条件。
[例4](2009年广东)已知二次函数 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点 到点
到点 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
分析:本题是探索使结论成立的条件,可根据题意步步等价转化,寻找成立的充要条件。如函数有零点 于方程有根
于方程有根 函数图像与
函数图像与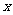 轴有交点。
轴有交点。
解:(1)依题可设 (
( ),则
),则 ;
;
又 的图像与直线
的图像与直线 平行
平行 

 ,
,  ,
,
设 ,则
,则

当且仅当 时,
时, 取得最小值,即
取得最小值,即 取得最小值
取得最小值
当 时,
时, 解得
解得
当 时,
时, 解得
解得
(2)由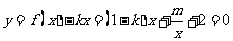 (
( ),得
),得

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当 时,方程
时,方程 有二解
有二解 ,
,
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
当 时,方程
时,方程 有一解
有一解 ,
,  ,
,
函数 有一零点
有一零点
综上,当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当 (
( ),或
),或 (
( )时,
)时,
函数 有两个零点
有两个零点 ;
;
当 时,函数
时,函数 有一零点
有一零点 .
.
4攻略之四--类比联想
类比是根据两事物的一些属性相同或相似推测另一些属性也可能相同或相似的认识方法,也是人类认识事物的普遍规律之一。所谓类比猜想的策略就是由一个问题的结论或解决方法类比猜想出另一个类似问题的结论或解决方法,并以严格论证。
[例5]将图表填完整
|
平面 |
空间 |
|
三角形两边之和大于第三边 |
三棱锥任意三个面的面积之和大于第四个面的面积 |
|
三角形的面积等于任意一边的长度与这边上高的乘积的一半 |
三棱锥的体积等于任意一个底面的面积与该底面上的高的乘积的三分之一 |
|
三角形的面积等于其内切圆半径与三角形周长的乘积的一半 |
|
解析:本题是平面与空间的类比,由已知前几组类比可得到如下信息:①平面中的三角形与空间中的三棱锥是类比对象;②三角形各边的边长与三棱锥的各面的面积是类比对象;③三角形边上的高与三棱锥面上的高是类比对象;④三角形的面积与三棱锥的体积是类比对象;⑤三角形的面积公式中的“二分之一”与三棱锥的体积公式中的“三分之一”是类比对象。
由上分析不难知道空格处应填:三棱锥的体积等于其内切球半径与三棱锥表面积的乘积的三分之一。对于这一结论的正确性,可以通过等体积法,将三棱锥分割成四个小的三棱锥去证明。
点评:平面到空间的类比是常见的类比形式,要掌握这些常见的类比方向,题目也就不难解决了。
预测2010年数学试卷中继续保持了探索型、开放型、研究型等题型,形式上也会有所突破,如只猜不证,只算不写等;填空题中出现了条件、结论完全开放的设计,题型的创新,带来了新的理念,这必将促进教学的创新。
探索性问题常常需要由给定的题设条件去探索相应的结论,或由问题的题干去追溯相应的条件,要求在解题之前必须透过问题的表象去寻找、去发现规律性的东西。问题增加了许多可变的因素,思维指向不明显,解题时往往难于下手。
近年来,探索性问题在高考试题中多次出现,主要有以下几类:
(1)探索条件型问题:从给定的问题结论出发,追溯结论成立的充分条件;
(2)探索结论型问题:从给定的题设条件出发,探求相关的结论;
(3)探索存在型问题:从假设相关结论存在出发,从而肯定或否定这种结论是否存在;
(4)探索综合型问题:从变更题设条件或问题的结论的某个部分出发,探究问题的相应变化。
24.(14分)如图所示,两根间距为L的金属导轨MN和PQ,电阻不计,左端向上弯曲,其余水平,水平导轨左端有宽度为d、方向竖直向上的匀强磁场I,右端有另一磁场II,其宽度也为d,但方向竖直向下,磁场的磁感强度大小均为B。有两根质量均为m、电阻均为R的金属棒a和b与导轨垂直放置,b棒置于磁场II中点C、D处,导轨除C、D两处(对应的距离极短)外其余均光滑,两处对棒可产生总的最大静摩擦力为棒重力的K倍,a棒从弯曲导轨某处由静止释放。当只有一根棒作切割磁感线运动时,它速度的减小量与它在磁场中通过的距离成正比,即 。
。
(1)若a棒释放的高度大于h0,则a棒进入磁场I时会使b棒运动,判断b 棒的运动方向并求出h0。
(2)若将a棒从高度小于h0的某处释放,使其以速度v0进入磁场I,结果a棒以 的速度从磁场I中穿出,求在a棒穿过磁场I过程中通过b棒的电量q和两棒即将相碰时b棒上的电功率Pb。
的速度从磁场I中穿出,求在a棒穿过磁场I过程中通过b棒的电量q和两棒即将相碰时b棒上的电功率Pb。
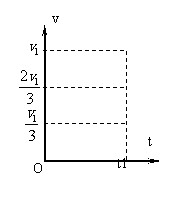
(3)若将a棒从高度大于h0的某处释放,使其以速度v1进入磁场I,经过时间t1后a棒从磁场I穿出时的速度大小为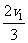 ,求此时b棒的速度大小,在如图坐标中大致画出t1时间内两棒的速度大小随时间的变化图像,并求出此时b棒的位置。
,求此时b棒的速度大小,在如图坐标中大致画出t1时间内两棒的速度大小随时间的变化图像,并求出此时b棒的位置。

23.(14分)两个带电量均为+q小球,质量均为m,固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上,另一端点用光滑铰链固定在O点,整个装置可以绕垂直于纸面的水平轴在竖直平面内自由转动。直角三角形的直角边长为L。
(1)若施加竖直向上的匀强电场E1,使框架OB边水平、OA边竖直并保持静止状态,则电场强度E1多大?在此电场中,此框架能否停止在竖直平面内任意位置?
(2)若改变匀强电场的大小和方向(电场仍与框架面平行),为使框架的OB边水平、OA边竖直(A在O的正下方),则所需施加的匀强电场的场强E2至少多大?方向如何?
(3)若施加竖直向上的匀强电场E3 ,并将A球的带电量改为-q,其余条件不变,试找出框架所有可能的平衡位置,求出OA边与竖直方向的夹角θ,并画出所对应的示意图。
,并将A球的带电量改为-q,其余条件不变,试找出框架所有可能的平衡位置,求出OA边与竖直方向的夹角θ,并画出所对应的示意图。
22. (12分)横截面积分别为SA=2.0×10-3m2、SB=1.0×10-3m2的汽缸A、B竖直放置,底部用细管连通,用质量分别为mA=4.0kg、mB=2.0kg的活塞封闭一定质量的气体,气缸A中有定位卡。当气体温度为27℃时,活塞A恰与定位卡环接触,此时封闭气体的体积为V0=300mL,外界大气压强为P0=1.0×105Pa。(g=10m/s2)
(12分)横截面积分别为SA=2.0×10-3m2、SB=1.0×10-3m2的汽缸A、B竖直放置,底部用细管连通,用质量分别为mA=4.0kg、mB=2.0kg的活塞封闭一定质量的气体,气缸A中有定位卡。当气体温度为27℃时,活塞A恰与定位卡环接触,此时封闭气体的体积为V0=300mL,外界大气压强为P0=1.0×105Pa。(g=10m/s2)
(1)当将气体温度缓慢升高到57℃时,封闭气体的体积多大?
(2)保持气体的温度57℃不变,用力缓慢压活塞B,使气体体积恢复到V0,求此时封闭气体的压强多大?此时活塞A与定位卡环间的弹力多大?

21.(12分)一物块以一定的初速度沿斜面向上滑出,利用DIS实验系统,在计算机屏幕上得到其速度大小随时间的变化关系图像如图所示。求:(g=10m/s2)
(1)物块上滑和下滑的加速度大小a1、a2。
(2)物块向上滑行的最大距离S。
(3)斜面的倾角θ及物块与斜面间的动摩擦因数μ。
20. (8分)(辨析题)如图所示,长为L的轻绳一端固定在O点,另一端系一质量为m的小球,在最低点给小球一水平初速度v0,同时对小球施加一大小不变,方向始终垂直于绳的力F,小球沿圆周运动到绳水平时,小球速度大小恰好也为v0。求F的大小。
(8分)(辨析题)如图所示,长为L的轻绳一端固定在O点,另一端系一质量为m的小球,在最低点给小球一水平初速度v0,同时对小球施加一大小不变,方向始终垂直于绳的力F,小球沿圆周运动到绳水平时,小球速度大小恰好也为v0。求F的大小。
下面是某位同学的分析:
小球在力F的作用下先加速后减速,由对称性可以判断,当轻绳向上摆起45°角时小球速度最大,切线方向的加速度为零,此时重力沿切线方向的分力与F等大反向,……。
该同学的分析正确吗?若正确,请根据该同学的分析思路,求出F的大小。
若不正确,请你分析并求出正确结果。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com