
2. 思想和方法:
1. 知识与技能:
2.判断下列函数的单调性,并求出单调区间:
⑴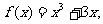
⑵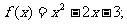
⑶
⑷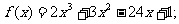
反思:你对利用导数去研究函数的单调性有什么看法?
※典例讲解:
例3:水以恒速注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间t的函数关系图象。
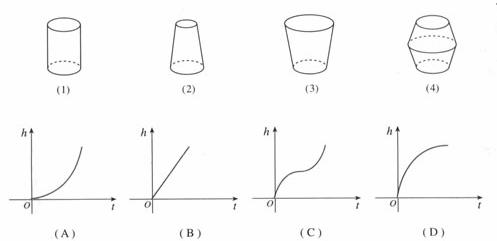
变式:若将例3中高度h和时间t的关系变为横坐标为高度h和纵坐标为体积V的关系,那么此题结论又将如何?
思考:对于此题你是怎样判断的,使用什么样的知识,结论如何呢?
※课堂练习:

※ 课堂小结:
※学习探究
探究任务一:函数单调性与其导数的关系:
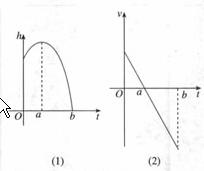 问题1:如图(1)表示高台跳水运动员的高度h随时间t变化的函数
问题1:如图(1)表示高台跳水运动员的高度h随时间t变化的函数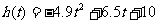 的图像,图(2)表示高台跳水运动员的速度
的图像,图(2)表示高台跳水运动员的速度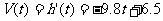 h的图像.
h的图像.
通过观察图像,你能发现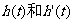 这两个函数图像有什么联系吗?
这两个函数图像有什么联系吗?
启发: 函数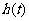 在(0,a)上位增函数,函数
在(0,a)上位增函数,函数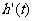 在(0,a)上有何特点呢?函数
在(0,a)上有何特点呢?函数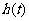 在(a,b)上位减函数函数,那么函数
在(a,b)上位减函数函数,那么函数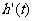 在(a,b)上有何特点呢?
在(a,b)上有何特点呢?
问题2:观察图(1)-图(4),探讨函数与其导函数是否也存在问题(1)的关系呢?
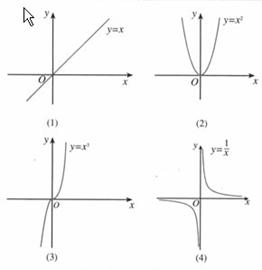
问题3:通过对问题1和问题2的观察,你能得到原函数的单调性与其导函数的正负号有何关系?你能得到怎样的结论?
问题4:上述结论主要是通过观察得到的,你能给予证明吗?
启发1:导数的几何意义为切线的斜率,你能从这个角度给予说明吗?
启发2:结合单调性的定义,你能从导数的定义出发予以说明吗?
探究任务二: 与函数单调性的关系:
与函数单调性的关系:
问题5:在区间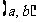 上
上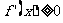 ,则函数
,则函数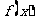 区间
区间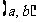 必为增函数,你认为这句话对吗?请说明理由.
必为增函数,你认为这句话对吗?请说明理由.
问题6:函数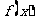 在区间
在区间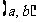 上为增函数,则在区间
上为增函数,则在区间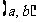 上
上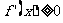 成立.你认为这句话对吗?说明理由.
成立.你认为这句话对吗?说明理由.
自主测评:
1. 已知导函数的下列信息:
当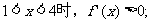
当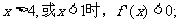
当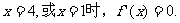
试画出函数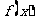 图像的大致形状.
图像的大致形状.
8.(2009北京卷理)
如图,在三棱锥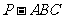 中,
中,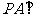 底面
底面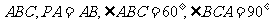 ,
,
点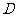 ,
,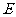 分别在棱
分别在棱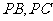 上,且
上,且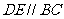

(Ⅰ)求证: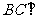 平面
平面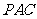 ;
;
(Ⅱ)当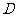 为
为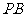 的中点时,求
的中点时,求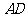 与平面
与平面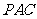 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点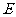 使得二面角
使得二面角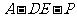 为直二面角?并说明理由.
为直二面角?并说明理由.
7. (2009全国卷Ⅱ文)(本小题满分12分)
|
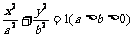
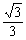
|

(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有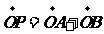 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
6. (2009浙江文)设等差数列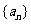 的前
的前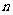 项和为
项和为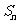 ,则
,则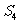 ,
, ,
,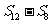 ,
,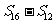 成等差数列。类比以上结论有:设等比数列
成等差数列。类比以上结论有:设等比数列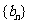 的前
的前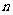 项积为
项积为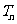 ,则
,则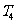 ,
, ,
,
, ,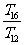 成等比数列。
成等比数列。
5.观察sin220°+cos250°+sin20°cos50°=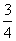 ,sin215°+cos245°+sin15°
,sin215°+cos245°+sin15°
·cos45°=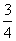 ,写出一个与以上两式规律相同的一个等式
.
,写出一个与以上两式规律相同的一个等式
.
4. (2009安徽卷理)若不等式组 所表示的平面区域被直线
所表示的平面区域被直线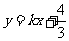 分为面积相等的两部分,则
分为面积相等的两部分,则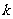 的值是
的值是
A.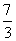 B.
B.  C.
C.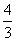 D.
D. 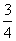
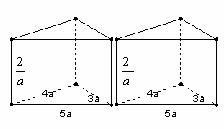
3. 如图,有两个相同的直三棱柱,高为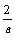 ,底面三角形的三边长别为3a,4a,5a(a>0)。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则a的取值范围是( )。
,底面三角形的三边长别为3a,4a,5a(a>0)。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则a的取值范围是( )。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com