
4、对于平面α和共面的直线m,n,下列命题中真命题是
(A)若m⊥α,m⊥n,则n∥α (B)若m∥α,n∥α,则m∥n
(C)若m α,n∥α,则m∥n
(D)若m、n与α所成角相等,则m∥n
α,n∥α,则m∥n
(D)若m、n与α所成角相等,则m∥n
3、已知命题P:|a|<2,且|b|<1,命题Q:|a-b|<1,命题P是命题Q的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
2、已知复数Z满足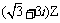 =3i,则Z等于
=3i,则Z等于
(A)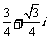 (B)
(B)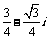 (C)
(C)  (D)
(D)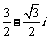
1、若全集U={1,2,3,4},M={1,2},N={2,3},则CU(M∪N)等于
(A){1,2,3,} (B){2} (C){1,3,4} (D){4}
22、(本小题满分14分)
已知数列{an}中,a1=1,an+1=2an+n-1(n∈N*).
(Ⅰ)证明:数列{an+n}是等比数列;
(Ⅱ)记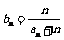 ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(Ⅲ)若 对一切n∈N*恒成立,求非零实数t的取值范围.
对一切n∈N*恒成立,求非零实数t的取值范围.
自贡市普高2010级第二次诊断性考试数学试卷(文)
21、(本小题满分12分)
已知中心在原点的椭圆C过点M(1,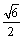 ),F(
),F(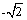 ,0)是椭圆C的左焦点,P,Q是椭圆C上的两个动点,且|PF|,|MF|,|QF|成等差数列.
,0)是椭圆C的左焦点,P,Q是椭圆C上的两个动点,且|PF|,|MF|,|QF|成等差数列.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)求证:线段PQ的垂直平分线经过一个定点A.
20、(本小题满分12分)
已知函数f(x)= x3+bx2-3a2x(a≠0)在x=a处取得极值.
x3+bx2-3a2x(a≠0)在x=a处取得极值.
(Ⅰ)用x,a表示f(x);
(Ⅱ)设函数g(x)=2x3-3af ′(x)-6a3,如果g(x)在区间(0,1)上存在极小值,求实数a的取值范围.
19、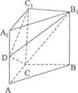 (本小题满分12分)
(本小题满分12分)
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.
(Ⅰ)若D为AA1的中点,求证:平面B1CD⊥B1C1D;
(Ⅱ)若二面角B1-DC-C1的大小为60°,求AD的长.
18、(本小题满分12分)
甲、乙两人进行某项对抗性游戏,采用“七局四胜制”即先赢四局者胜,若甲、乙两人水平相同,且已知甲先赢了前两局.
(Ⅰ)求乙取胜的概率;
(Ⅱ)求比赛进行完七局的概率.
17、(本小题满分12分)
已知函数f(x)=sin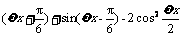 (x∈R,ω>0)
(x∈R,ω>0)
(Ⅰ)求函数f(x)的值域;
(Ⅱ)若x=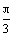 是函数f(x)的图像的一条对称轴且1<ω<5,求f(x)的单调递增区间.
是函数f(x)的图像的一条对称轴且1<ω<5,求f(x)的单调递增区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com