2．从1950年到2000年的半个世纪中，四个城市年平均气温变化的整体趋势是

　　 A．时高时低　　 B．不断降低　　 C．不断升高　　 D．没有变化

　　 图2是某地等高线地形图，读图回答3-5题．　　

1．图中①-④表示的城市是　

　　 A．广州、沈阳、昆明、乌鲁木齐　　 B．广州、昆明、乌鲁木齐、沈阳

　　 C．昆明、广州、乌鲁木齐、沈阳　　 D．昆明、广州、沈阳、乌鲁木齐

22、(本小题满分14分)

　　 已知点P在曲线C：y=(x>1)上，设曲线C在点P处的切线为l，若l与函数y=kx(k>0)的图像的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为x_A、x_B，记f(t)=x_A·x_B．

　　 (Ⅰ)求f(t)的解析式；　　

　　 (Ⅱ)设数列{a_n}(n≥1，n∈N)满足a₁=1，a_n=(n≥2)，数列{b_n}满足b_n=，求a_n与b_n；　　

(Ⅲ)在(Ⅱ)的条件下，当1<k<3时，证明不等式：a₁+a₂+…+a_n>．

自贡市普高2010级第二次诊断性考试数学试卷(理)

21、(本小题满分12分)

　　 已知F₁、F₂是椭圆(a>b>0)的左、右焦点，点P在椭圆上，线段PF₂与y轴的交点M满足．

　　 (Ⅰ)求椭圆的标准方程；

　　 (Ⅱ)过F₂作不与x轴重合的直线l，l与圆x²+y²=a²+b²相交于A、B并与椭圆相交于C、D，当=λ，且λ∈时，求△F₁CD的面积S的取值范围．

20、(本小题满分12分)

　　 已知A、B、C是直线l上的三点，O是直线l外一点，向量满足=[f(x)+2f ′(1)]-ln(x+1)．

　　 (Ⅰ)求函数y=f(x)的表达式；　　

　　 (Ⅱ)若x>0，证明：f(x)>；

　　 (Ⅲ)若不等式x²≤f(x²)+m²-2m-3对x∈[-1，1]恒成立，求实数m的取值范围．

19、(本小题满分12分)

如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，2AC=AA₁=BC=2．　　

　　 (Ⅰ)若D为AA₁的中点，求证：平面B₁CD⊥B₁C₁D；

　　 (Ⅱ)若二面角B₁-DC-C₁的大小为60°，求AD的长．

18、(本小题满分12分)

　　 把圆周4等分，A是其中一个分点，动点P在四个分点上按逆时针方向前进。投掷一个质地均匀的正四面体，它的四个面上分别写着1，2，3，4四个数字，P从A点出发，按照正四面体底面上所投掷的点数前进(数字为n就前进n个分点)，转一周之前继续投掷．

(Ⅰ)求点P恰好返回到A点的概率：

　　 (Ⅱ)在点P转一周能返回A点的所有结果中，用随机变量ζ表示点P返回A点时的投掷次数，求ζ的分布列和期望．

17、(本小题满分12分)

　　 已知函数f(x)=sin(ωx+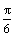)+sin(ωx-)-2cos²(x∈R，ω>0)

　　 (Ⅰ)求函数f(x)的值域；

　　 (Ⅱ)若x=是函数f(x)的图像的一条对称轴且1<ω<5，求f(x)的单调递增区间．

16、下列四个命题中，真命题的序号有__________(写出所有真命题的序号)．

　 (1)将函数y=|x+1|的图象按向量=(-1，0)平移，得到的图象的对应函数表达式为 y=|x|

　 (2)圆x²+y²+4x-2y+1=0与直线y=相交，所得弦长为2．　　

　 (3)若sin(α+β)=，sin(α-β)=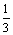，则tanα·cotβ=5．

　 (4)已知正方体ABCD-A₁B₁C₁D₁，P为底面ABCD内一动点，P到平面AA₁D₁D的距离与到直线CC₁的距离相等，则P点的轨迹是抛物线的一部份．

15、有红、黄、蓝三种颜色的小球各5个，都分别标有字母A、B、C、D、E，现取出5个，要求字母各不相同且三种颜色齐备，则有_________种取法(用数字做答)．