3. 分析下列情况中系统的动量是否守恒(　　 )

A．如图2所示，小车停在光滑水平面上，车上的人在车上走动时，对人与车组成的系统

B．子弹射入放在光滑水平面上的木块中对子弹与木块组成的系统(如图3)

C．子弹射入紧靠墙角的木块中，对子弹与木块组成的系统

D．斜向上抛出的手榴弹在空中炸开时

[错解分析]错解：本题的错解在于漏掉了一些选项，由于对动量守恒条件中的合外力为零认识不清，混淆了内力和外力而漏选了B。由于没有考虑到爆炸过程是一个作用时间阶段，内力远大于外力的过程，符合动量守恒的近似条件，而漏选了D。

[解题指导]动量守恒定律成立的条件：(1)系统不受外力作用时，系统动量守恒；(2)系统所受合外力之和为0，则系统动量守恒；(3)系统所受合外力虽然不为零，但系统内力远大于外力时，系统的动量看成近似守恒。

[答案]本题的正确选项为A、B、D。A、B选项符合条件(2)；D选项符合条件(3)

2. 质量为M的小车在水平地面上以速度v₀匀速向右运动。当车中的砂子从底部的漏斗中不断流下时，车子的速度将(　　 )

A. 减小　　　　　 B. 不变　　　　 C. 增大　　　　 D. 无法确定

[错解分析]错解：因为随着砂子的不断流下，车子的总质量减小，根据动量守恒定律总动量不变，所以车速增大，故选C。

产生上述错误的原因，是在利用动量守恒定律处理问题时，研究对象的选取出了问题。因为，此时，应保持初、末状态研究对象的是同一系统，质量不变。

[解题指导]利用动量守恒定律解决问题的时候，在所研究的过程中，研究对象的系统一定不能发生变化，抓住研究对象，分析组成该系统的各个部分的动量变化情况，达到解决问题的目的。

[答案]本题的正确选项为B。

本题中砂子和车组成的系统动量守恒，由动量守恒定律，在初状态，砂子下落之前，砂子和车都以v₀向前运动；在末状态，由于惯性，砂子下落的时候具有和车相同的水平速度v₀，车的速度为v’，由(M+m)v₀=m v₀+M v’得v’= v₀，车速不变,故B正确。

复习指导：①回归课本夯实基础，仔细看书把书本中的知识点掌握到位

　　　　 　②练习为主提升技能，做各种类型的习题，在做题中强化知识

　　　　　 ③整理归纳举一反三，对易错知识点、易错题反复巩固

　　　　　 ④应用动量守恒定律的注意点：

⑴矢量性：动量守恒定律的数学表达式是个矢量关系式.对于我们常见作用前后物体的运动方向都在同一直线上的问题，可选取一个正方向，凡与正方向相同的矢量均取正值，反之为负，这样即可将矢量运算简化为代数运算．

⑵同时性：动量守恒指系统在任一瞬间的动量恒定。等号左边是作用前系统内各物体动量在同一时刻的矢量和，等号右边是作用后系统内各物体动量在另一同时刻的矢量和．不是同一时刻的动量不能相加．

⑶相对性：表达式中各物体的速度(动量)必须是相对于同一惯性参考系而言的，一般均以地面为参考系．若题设条件中各速度不是同一参考系的速度，就必须经过适当转换，使其成为同一参考系的速度值．

⑷系统性：解题时，选择的对象是满足条件的系统，不是其中一个物体，初、末两个状态研究对象必须一致。

⑸广泛性：动量守恒定律具有广泛的适用范围，不论物体间的相互作用力性质如何；不论系统内部物体的个数；不论它们是否互相接触；不论相互作用后物体间是粘合还是分裂,只要系统所受合外力为零,动量守恒定律都适用。动量守恒定律既适用于低速运动的宏观物体,也适用于高速运动的微观粒子间的相互作用,大到天体,小到基本粒子间的相互作用都遵守动量守恒定律。　

⑤应用动量守恒定律解题的一般步骤：

⑴确定研究对象，选取研究过程；

⑵分析内力和外力的情况，判断是否符合守恒条件；

⑶选定正方向，确定初、末状态的动量，

⑷根据动量守恒定律列方程求解。

应用时，无需分析过程的细节，这是它的优点所在，定律的表述式是一个矢量式，应用时要特别注意方向。

1. 在光滑水平面上停放着两木块A和B，A的质量大，现同时施加大小相等的恒力F使它们相向运动，然后又同时撤去外力F，结果A和B迎面相碰后合在一起，问A和B合在一起后的运动情况将是(　　 )

A.停止运动　　　　　　　　　 B.因A的质量大而向右运动

C.因B的速度大而向左运动　　 D.运动方向不能确定

[错解分析]错解：因为A的质量大，所以它的惯性大，所以它不容停下来，因此应该选B；或者因为B的速度大，所以它肯定比A后停下来，所以应该选C。

产生上述错误的原因是没有能够全面分析题目条件，只是从一个单一的角度去思考问题，失之偏颇。

[解题指导]碰撞问题应该从动量的角度去思考，而不能仅看质量或者速度，因为在相互作用过程中，这两个因素是一起起作用的。

[答案]本题的正确选项为A。

由动量定理知，A和B两物体在碰撞之前的动量等大反向，碰撞过程中动量守恒，因此碰撞之后合在一起的总动量为零，故选A。

6. 木块a和b用一根轻弹簧连接起来，放在光滑水平面上，a紧靠在墙壁上，在b上施加向左的水平力使弹簧压缩，如图1所示，当撤去外力后，下列说法中正确的是(　　 )

A．a尚未离开墙壁前，a和b系统的动量守恒

B．a尚未离开墙壁前，a与b系统的动量不守恒

C．a离开墙后，a、b系统动量守恒

D．a离开墙后，a、b系统动量不守恒

点拨：此题考查动量守恒定律应用的条件。正确选项为BC。

5. A、B两球在光滑水平面上沿同一直线、同一方向运动，A球的动量是5kg﹒m/s，B球的动量是7kg﹒m/s，当A球追上B球时发生碰撞，则碰撞后A、B两球的动量可能值是(　　 )

　　 　A．6kg﹒m/s、6kg﹒m/s　　　 B．4kg﹒m/s、8kg﹒m/s

　　 　C．-2kg﹒m/s、14kg﹒m/s　　 D．-3kg﹒m/s、15kg﹒m/s

点拨：此题考查碰撞的规律。必须满足动量守恒定律、动能不增加、符合实际情景选A。

4. 如图所示，在光滑的水平面上，依次放着质量均为m的4个小球，小球排列在一条直线上，彼此间隔一定的距离。开始时后面3个小球处于静止状态，第一个小球以速度v向第二个小球碰去，结果它们先后都粘合到一起向前运动。由于连续碰撞，系统剩余的机械能是 __________。

点拨：此题考查多物体多过程动量守恒和能量守恒定律。答案：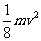

3. 下列关于动量守恒的论述正确的是

A．某物体沿着斜面下滑，物体的动量守恒

B．系统在某方向上所受的合外力为零，则系统在该方向上动量守恒

C．如果系统内部有相互作用的摩擦力，系统的机械能必然减少，系统的动量也不再守恒

D．系统虽然受到几个较大的外力，但合外力为零，系统的动量仍然守恒

点拨：此题考查动量守恒的条件。选BD。

2. 一辆小车在光滑的水平上匀速行使，在下列各种情况中，小车速度仍保持不变的是(　　 )

A．从车的上空竖直掉落车内一个小钢球

B．从车厢底部的缝隙里不断地漏出砂子

C．从车上同时向前和向后以相同的对地速率扔出质量相等的两物体

D. 从车上同时向前和向后以相同的对车速率扔出质量相等的两物体

　点拨：此题考查动量守恒定律。选BD。

针对典型精析的例题题型，训练以下习题。

1. A、B两球在光滑水平面上相向运动，两球相碰后有一球停止运动，则下述说法中正确的是 (　　 )

A．若碰后，A球速度为0，则碰前A的动量一定大于B的动量

B．若碰后，A球速度为0，则碰前A的动量一定小于B的动量

C．若碰后，B球速度为0，则碰前A的动量一定大于B的动量

D．若碰后，B球速度为0，则碰前A的动量一定小于B的动量

点拨： 此题考查动量守恒定律的公式。选AD

题型1.(子弹射木块题型)矩形滑块由不同材料的上下两层固体组成，将其放在光滑的水平面上，质量为m的子弹以速度v水平射向滑块。若射中上层子弹刚好不穿出，若射中下层子弹刚好能嵌入，那么(　　 )

　　 A．两次子弹对滑块做的功一样多　　 B．两次滑块所受冲量一样大

C．子弹嵌入上层时对滑块做功多　　 D．子弹嵌入上层时滑块所受冲量大

解：设固体质量为M，根据动量守恒定律有：

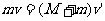
由于两次射入的相互作用对象没有变化，子弹均是留在固体中，因此，固体的末速度是一样的，而子弹对滑块做的功等于滑块的动能变化，对滑块的冲量等于滑块的动量的变化，因此A、B选项是正确的。

规律总结：解决这样的问题，还是应该从动量的变化角度去思考，其实，不管是从哪个地方射入，相互作用的系统没有变化，因此，动量和机械能的变化也就没有变化。

题型2.(动量守恒定律的判断)把一支枪水平固定在小车上，小车放在光滑的水平地面上，枪发射出子弹时，关于枪、子弹、车的下列说法正确的是(　　 )

A.枪和子弹组成的系统动量守恒

B.枪和车组成的系统动量守恒

C.只有忽略不计子弹和枪筒之间的摩擦，枪、车和子弹组成的系统的动量才近似守恒

D.枪、子弹、车组成的系统动量守恒

解：本题C选项中所提到的子弹和枪筒之间的摩擦是系统的内力，在考虑枪、子弹、车组成的系统时，这个因素是不用考虑的。根据受力分析，可知该系统所受合外力为0，符合动量守恒的条件，故选D

规律总结：判断系统是否动量守恒时，一定要抓住守恒条件，即系统不受外力或者所受合外力为0。

题型3.(碰撞中过程的分析)如图所示，位于光滑水平桌面上的小滑块A和B都可视作质点，质量相等。B与轻质弹簧相连。设B静止，A以某一初速度向B运动并与弹簧发生碰撞。在整个碰撞过程中，弹簧具有的最大弹性势能等于(　　 )

A. A的初动能

B. A的初动能的1/2

C. A的初动能的1/3

D. A的初动能的1/4

解： 解决这样的问题，最好的方法就是能够将两个物体作用的过程细化。具体分析如右图，开始A物体向B运动，如右上图；接着，A与弹簧接触，稍有作用，弹簧即有形变，分别对A、B物体产生如右中图的作用力，对A的作用力的效果就是产生一个使A减速的加速度，对B的作用力的效果则是产生一个使B加速的加速度。如此，A在减速，B在加速，一起向右运动，但是在开始的时候，A的速度依然比B的大，所以相同时间内，A走的位移依然比B大，故两者之间的距离依然在减小，弹簧不断压缩，弹簧产生的作用力越来越大，对A的加速作用和对B的加速作用而逐渐变大，于是，A的速度不断减小，B的速度不断增大，直到某个瞬间两个物体的速度一样，如右下图。过了这个瞬间，由于弹簧的压缩状态没有发生任何变化，所以对两个物体的作用力以及力的效果也没有变，所以A要继续减速，B要继续加速，这就会使得B的速度变的比A大，于是A、B物体之间的距离开始变大。因此，两个物体之间的距离最小的时候，也就是弹簧压缩量最大的时候，也就是弹性势能最大的时候，也就是系统机械能损失最大的时候，就是两个物体速度相同的时候。

根据动量守恒有，根据能量守恒有，以上两式联列求解的，可见弹簧具有的最大弹性势能等于滑块A原来动能的一半，B正确

规律总结：处理带有弹簧的碰撞问题，认真分析运动的变化过程是关键，面对弹簧问题，一定要注重细节的分析，采取“慢镜头”的手段。

题型4.(动量守恒定律的适用情景)小型迫击炮在总质量为1000kg的船上发射，炮弹的质量为2kg．若炮弹飞离炮口时相对于地面的速度为600m/s，且速度跟水平面成45°角，求发射炮弹后小船后退的速度？

解：发射炮弹前，总质量为1000kg的船静止，则总动量Mv=0．

发射炮弹后，炮弹在水平方向的动量为mv₁'cos45°，船后退的动量为(M-m)v₂'．

据动量守恒定律有

0=mv₁'cos45°+(M-m)v₂'．

取炮弹的水平速度方向为正方向，代入已知数据解得

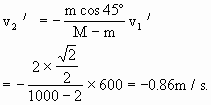
规律总结：取炮弹和小船组成的系统为研究对象，在发射炮弹的过程中，炮弹和炮身(炮和船视为固定在一起)的作用力为内力．系统受到的外力有炮弹和船的重力、水对船的浮力．在船静止的情况下，重力和浮力相等，但在发射炮弹时，浮力要大于重力．因此，在垂直方向上，系统所受到的合外力不为零，但在水平方向上系统不受外力(不计水的阻力)，故在该方向上动量守恒．

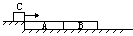题型5. (多物体多过程动量守恒)两块厚度相同的木块A和B，并列紧靠着放在光滑的水平面上，其质量分别为m_A=2.0kg，m_B=0.90kg．它们的下底面光滑，上表面粗糙．另有质量_C=0.10kg的铅块C(其长度可略去不计)以v_C=10m/s的速度恰好水平地滑到A的上表面(见图)，由于摩擦，铅块最后停在本块B上，测得B、C的共同速度为v=0.50m/s，求：木块A的速度和铅块C离开A时的速度．

解：设C离开A时的速度为v_C，此时A、B的共同速度为v_A，对于C刚要滑上A和C刚离开A这两个瞬间，由动量守恒定律知

m_Cv_C=(m_A+m_B)v_A+m_Cv'_C (1)

以后，物体C离开A，与B发生相互作用．从此时起，物体A不再加速，物体B将继续加速一段时间，于是B与A分离．当C相对静止于物体B上时，C与B的速度分别由v'_C和v_A变化到共同速度v．因此，可改选C与B为研究对象，对于C刚滑上B和C、B相对静止时的这两个瞬间，由动量守恒定律知

m_Cv'_C+m_Bv_A=(m_B+m_C)v　　 (2)

由(l)式得　　　　　　　 m_Cv'_C=m_Cv_C-(m_A+m_B)v_A

代入(2)式　　　　　　　 m_Cv'_C-(m_A+m_C)v_A+m_Bv_A=(m_B+m_C)v．

得木块A的速度

所以铅块C离开A时的速度

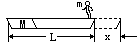题型6.(人船模型)在静止的湖面上有一质量M=100kg的小船，船上站立质量m=50kg的人，船长L=6m，最初人和船静止．当人从船头走到船尾(如图)，船后退多大距离？(忽略水的阻力)

解：选地球为参考系，人在船上行走，相对于地球的平均速度为(L-x)/t，船相对于地球后退的平均速度为x/t，系统水平方向动量守恒方程为

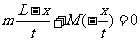　　 故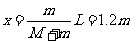　　　

规律总结：错解：由船和人组成的系统，当忽略水的阻力时，水平方向动量守恒．取人前进的方向为正方向，设t时间内人由船头走到船尾，则人前进的平均速度为L/t，船在此时间内后退了x距离，则船后退的平均速度为x/t，水平方向动量守恒方程为

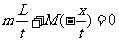　　 故　　

这一结果是错误的，其原因是在列动量守恒方程时，船后退的速度x/t是相对于地球的，而人前进的速度L/t是相对于船的。相对于不同参考系的速度代入同一公式中必然要出错．

题型7. (动量守恒中速度的相对性)一个静止的质量为M的原子核，放射出一个质量为m 的粒子，粒子离开原子核时相对于核的速度为v₀，原子核剩余部分的速率等于(　　 )

解：取整个原子核为研究对象。由于放射过程极为短暂，放射过程中其他外力的冲量均可不计，系统的动量守恒．放射前的瞬间，系统的动量p₁=0，放射出粒子的这一瞬间，设剩余部分对地的反冲速度为v'，并规定粒子运动方向为正方向，则粒子的对地速度v=v₀-v'，系统的动量

p₂=mv-(M-m)v'=m(v₀-v')-(M-m)v'．

由p₁=p₂，即

0=m(v₀-v)-(M-m)v'=mv₀-Mv'．

故选C。

规律总结：运用动量守恒定律处理问题，既要注意参考系的统一，又要注意到方向性