
8.注意辨析“系数”与“二项式系数”的区别;二项式系数和=2n,其中奇数项的二项式系数和=偶数项的二项式系数和=2n-1,二项式系数先增后减,并关于中间项“对称”,二项展开式中,中间项二项式系数最大;求二项展开式中系数绝对值最大的项,用“夹逼法”。
[举例]若 展开式中奇数二项式系数和为8192,则展开式中系数最大的项为
。
展开式中奇数二项式系数和为8192,则展开式中系数最大的项为
。
解析: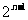 =8192得
=8192得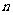 =14,则
=14,则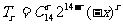 ,由于
,由于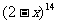 展开式中各项系数正负相间,故先求其展开式中系数绝对值最大的项,记为第
展开式中各项系数正负相间,故先求其展开式中系数绝对值最大的项,记为第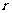 +1项,于是有:
+1项,于是有:
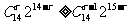 ①,
①,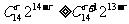 ②;由①②解得:4≤
②;由①②解得:4≤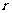 ≤5;
≤5;
又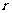 =5时系数为负,∴
=5时系数为负,∴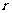 =4,即展开式中系数最大的项为
=4,即展开式中系数最大的项为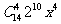 。
。
[巩固]若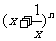 展开式的二项式系数之和为64,则展开式的常数项为( )
展开式的二项式系数之和为64,则展开式的常数项为( )
(07高考重庆理科第4题)
A.10 B.20 C.30 D.120
7.二项式定理的核心是展开式的通项,Tr+1=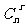 an-rbr(通项是展开式的第r+1项), r=0,1,2…n ,二项展开式共有n+1项。展开式的通项中根式宜用分数指数表示。审题是要注意所求的是“项”还是“第几项”还是“项的系数”。
an-rbr(通项是展开式的第r+1项), r=0,1,2…n ,二项展开式共有n+1项。展开式的通项中根式宜用分数指数表示。审题是要注意所求的是“项”还是“第几项”还是“项的系数”。
[举例]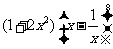 的展开式中常数项为 .(07高考全国Ⅱ卷理科第13题)
的展开式中常数项为 .(07高考全国Ⅱ卷理科第13题)
解析:先求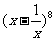 的展开式中常数项以及含x -2的项;
的展开式中常数项以及含x -2的项;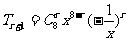 =
=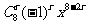
由8-2r=0得r=4, 由8-2r=-2得r=5;即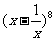 的展开式中常数项为
的展开式中常数项为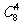 ,含x -2的项为
,含x -2的项为
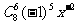 ;∴
;∴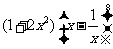 的展开式中常数项为
的展开式中常数项为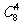 -2
-2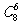 =
=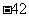
[巩固] 若 的展开式中含有常数项,则最小的正整数n等于 。
的展开式中含有常数项,则最小的正整数n等于 。
(07高考安徽理科第12题)
[迁移]f(x)=(x+1)n,且f ′ (x)展成关于x的多项式后x2的系数为60,则n= ( )
A.7 B.6 C.5 D.4
6.“抽象化归”是解决排列组合问题的“太极拳”,“逐一列举”是解决排列组合问题的“撒手锏”;有时,画“树状图”能使“逐一列举”变得更加简明、直观。
[举例1]已知两个实数集合A={a1,a2,…,a100},B={b1,b2, …,b50},若从A到B的映射f使得B中每个元素都有原象,且f( a1)≤f(a2)≤…≤f(a100),这样的映射共有 个。(用符号作答)。
解析:本题直接考虑集合A中每一个元素在B中的象的情况非常困难。注意到集合B中每个元素都有原象,即A中有50“组”元素分别与B中的50个元素对应;现将集合A中的100个元素按原有的顺序分成50组,每组至少一个元素;将集合B中的元素按从小到大的顺序排列为B={b1/,b2/, …,b50/};∵f( a1)≤f(a2)≤…≤f(a100),∴A中的“第1组”元素的象为b1/,“第2组”元素的象为b2/,…,“第50组”元素的象为b50/,此处没有排列的问题,即只要A中元素的分组确定了,映射也就随之确定了;而A中元素的分组可视为在由这100个元素所形成的99个“空”中插上49块“挡板”,所以有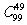 种分法,即映射共有
种分法,即映射共有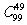 个。
个。
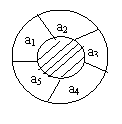 [举例2]一个同心圆形花坛分为两个部分,如右图,中间小圆部分
[举例2]一个同心圆形花坛分为两个部分,如右图,中间小圆部分
种植草坪,周围的圆环分成5等份为a1,a2,a3,a4,a5,种植红、黄、
蓝三色不同的花,要求相邻两部分种植不同颜色的花,则不同的
种植的方法为 种。
 解析:本题解法甚多,这里介绍画“树状图”列举法。
解析:本题解法甚多,这里介绍画“树状图”列举法。
在右图中,区域a1种红花,a2种黄花时共有5种不同
的种植方法;而区域a2种蓝花与种黄花情况相同,区
域a1种蓝花、黄花与种红花情况相同;故所有不同的
种植的方法为:3×2×5=30种
[巩固1]显示屏有一排7个小孔,每个小孔可显示0或
1,若每次显示其中3个孔,但相邻的两孔不能同时显
示,则该显示屏能显示信号的种数共有( )种
A.10 B.48 C.60 D.80
[巩固2] 函数f:{1,2,3} {1,2,3}满足f(f(x))= f(x),则这样的函数个数共有( )
{1,2,3}满足f(f(x))= f(x),则这样的函数个数共有( )
(A)1个 (B)4个 (C)8个 (D)10个
5.熟悉几个排列组合问题的基本模型:①部分元素“相邻”(捆绑法),②部分元素“不相邻”(用要求“不相邻”的元素插空),③部分元素有顺序(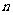 个元素全排,其中
个元素全排,其中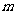 个元素要求按给定顺序排列的方法数为
个元素要求按给定顺序排列的方法数为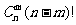 =
= ),④平均分组(
),④平均分组(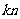 个元素平均分成
个元素平均分成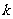 组的方法数为
组的方法数为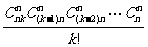 ),⑤相同元素分组(用“挡板法”)等。
),⑤相同元素分组(用“挡板法”)等。
[举例1]某校安排6个班到3个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 种。
解析:先将6个班分成3组,在将3个组分到3个工厂。6个班分成3组,从每组的人数看有3类:①4,1,1,有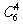 种;②3,2,1,有
种;②3,2,1,有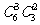 种,③2,2,2,有
种,③2,2,2,有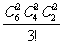 种;
种;
故不同的安排方法共有:(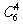 +
+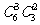 +
+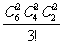 )×
)×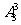 =540种。
=540种。
[举例2]某文艺小分队到一个敬老院演出,原定6个节目,后应老人们的要求决定增加3个节目,但原来六个节目的顺序不变,且新增的3个既不在开头也不在结尾,则这台演出共有
种不同的演出顺序。
解析:思路一:着眼于“位置”。从9个“位置”中选出6个,安排原来的6个节目,且第1和第9两个位置必须选,而他们的顺序是既定的,无需排列,所以有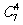 种方法,剩下的3个位置安排新增的3个节目,有
种方法,剩下的3个位置安排新增的3个节目,有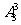 种方法;故所有不同的演出顺序有:
种方法;故所有不同的演出顺序有: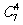
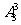 =210种。
=210种。
思路二:在原有6个节目的基础上“插空”。原来6个节目形成7个“空”,但前后两“空”不能安排,共有3类情况:①新增的3个节目互不相邻,有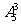 种方法;②新增的3个节目恰有两个相邻,有
种方法;②新增的3个节目恰有两个相邻,有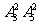 种方法;③新增的3个节目相邻,有5
种方法;③新增的3个节目相邻,有5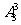 种方法,故所有不同的演出顺序有:
种方法,故所有不同的演出顺序有: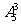 +
+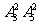 +5
+5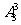 =210种。
=210种。
[巩固1]记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( ) (07高考北京理科第5题)
A.1440种 B.960种 C.720种 D.480种
[巩固2]学号为1,2,3,4的四名学生的考试成绩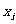 ∈{89,90,91,92,93}(
∈{89,90,91,92,93}(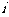 =1,2,3,4)且满足
=1,2,3,4)且满足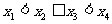 ,则这四为同学考试成绩所有可能的情况有 种。
,则这四为同学考试成绩所有可能的情况有 种。
[巩固3]现有10个市级“三好生”名额分配给高三八个班级,每班至少1个,则有
种不同的分配方案。
4.解决排列组合问题还要遵循“先选后排”、“正难则反”(即去杂法)等原则;
[举例]某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“ ”到“
”到“ ”共
”共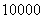 个号码.公司规定:凡卡号的后四位带有数字“
个号码.公司规定:凡卡号的后四位带有数字“ ”或“
”或“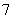 ”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( )(福建文科第12题)
”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( )(福建文科第12题)
A. B.
B.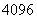 C.
C.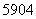 D.
D.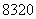
解析:直接考虑带有数字“ ”或“
”或“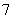 ”的情况太多,逐一讨论非常麻烦;考虑事件的反面:后四位不带有数字“
”的情况太多,逐一讨论非常麻烦;考虑事件的反面:后四位不带有数字“ ”或“
”或“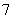 ”的,有84个,故“优惠卡”的个数为104-84=
”的,有84个,故“优惠卡”的个数为104-84=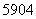 。
。
[巩固]四位同学乘坐一列有6节车厢的动车组,则他们至少有两人在同一节车厢的的情况共有 种?(用数字作答).
3.对“按某种要求将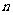 个元素排到
个元素排到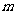 个位置”的问题,首先要确定研究的“抓手”:抓住元素还是抓住位置研究;再按特殊元素(特殊位置)优先的原则进行。
个位置”的问题,首先要确定研究的“抓手”:抓住元素还是抓住位置研究;再按特殊元素(特殊位置)优先的原则进行。
[举例] 从5位同学中选派4位同学在星期四到星期日参加公益活动,每人一天,其中甲不能安排在星期六,乙不能安排在星期天,则不同的选派方法共有 种。
解析:本题要完成的事件是:从5个不同的元素中选出4个元素,并按要求排在四个不同的位置。本题不宜抓住元素研究,因为每一个元素都不一定被选到,而每一个位置上都一定要有一个元素,故应该抓住位置研究。先看星期六(特殊位置,优先):不能安排甲,可以安排乙(特殊元素,优先)或除甲乙之外的一个同学,①安排乙:其它位置可任意安排,有
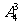 种,②不安排乙:可以安排其他三位同学,星期日可以安排甲或另外两个同学,星期四、五可任意安排,有
种,②不安排乙:可以安排其他三位同学,星期日可以安排甲或另外两个同学,星期四、五可任意安排,有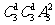 种,故不同的选派方法共有:
种,故不同的选派方法共有: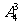 +
+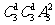 =78种。
=78种。
[巩固]四个不同的小球全部放入编号为1、2、3、4的四个盒中。(1)恰有两个空盒的放法有 种;(2)甲球只能放入2号或3好盒,而乙球不能放入4号盒的不同放法有 种。
2.解排列组合应用题首先要明确需要完成的事件是什么;其次要辨析完成该事件的过程:分类相加(每一类方法都能独立地完成这件事),分步相乘(每一步都不能完成事件,只有各个步骤都完成了,才能完成事件);较为复杂的事件往往既要分类,又要分步(每一类办法又都需分步实施);分类讨论是研究排列组合问题的重要思想方法之一,分类时要选定讨论对象、确保不重不漏。
[举例] 设集合I={1,2,3,4,5},选择I的两个非空子集A和B,要使B中最小的数大于A中的最大数,则不同的选择方法共有:( )种
A.50种 B.49种 C.48种 D.47种
解析:本题要完成的事件是:构造集合I的两个非空子集;要求:B中最小的数大于A中的最大数;显然B中的最小数不可能是1,以下分类:① B中的最小数是2,B中可以有{2,3,4,5}中的1个元素、2个元素、3个元素或4个元素,所有可能的情况有: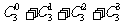 =8种,此时A只有{1}这1种;集合A、B都确定了,才算完成事件,∴完成事件有8×1=8中方法;② B中的最小数是3,B中可以有{3,4,5}中的1个元素、2个元素或3个元素,所有可能的情况有:
=8种,此时A只有{1}这1种;集合A、B都确定了,才算完成事件,∴完成事件有8×1=8中方法;② B中的最小数是3,B中可以有{3,4,5}中的1个元素、2个元素或3个元素,所有可能的情况有: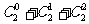 =4种,此时A中可以有{1,2}中的有1个元素或2个元素,有
=4种,此时A中可以有{1,2}中的有1个元素或2个元素,有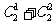 =3种,∴完成事件有4×3=12种方法;③ B中的最小数是4,B中可以有{4,5}中的1个元素或2个元素,所有可能的情况有2种,此时A中可以有{1,2,3}中的有1个元素、2个元素或3个元素,有
=3种,∴完成事件有4×3=12种方法;③ B中的最小数是4,B中可以有{4,5}中的1个元素或2个元素,所有可能的情况有2种,此时A中可以有{1,2,3}中的有1个元素、2个元素或3个元素,有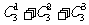 =7种,∴完成事件有2×7=14种方法;④ B中的最小数是5,只有{5}这1种,此时A中可以有{1,2,3,4}中的有1个元素、2个元素、3个元素或4个元素,有
=7种,∴完成事件有2×7=14种方法;④ B中的最小数是5,只有{5}这1种,此时A中可以有{1,2,3,4}中的有1个元素、2个元素、3个元素或4个元素,有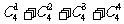 =15种,∴完成事件有1×15=15种方法;故完成事件的方法总数为:8+12+14+15=49,选B。
=15种,∴完成事件有1×15=15种方法;故完成事件的方法总数为:8+12+14+15=49,选B。
[巩固]从集合{O,P,Q,R,S}与{0,1,2,3,4,5,6,7,8,9}中各任选2个元素排成一排(字母和数字均不能重复).每排中字母O,Q和数字0至多只能出现一个的不同排法种数是_________.(用数字作答).
1. 熟悉排列数、组合数的计算公式;了解排列数、组合数的一些性质:①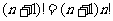 ,
,
由此可得: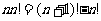 ,
, ,为相应的数列求和创造了条件;
,为相应的数列求和创造了条件;
②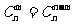 ;③
;③ ,由此得:
,由此得: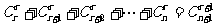 ;
;
[举例] 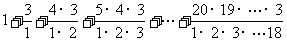 =___________
=___________
解析:原式=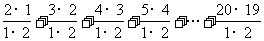 ;记
;记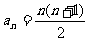 ,数列{
,数列{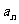 }的前19项和即为所求。记数列{
}的前19项和即为所求。记数列{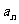 }的前
}的前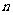 项和为
项和为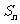 ;该数列的求和办法有很多种,但都比较烦琐,这里介绍用组合数性质求解:注意到
;该数列的求和办法有很多种,但都比较烦琐,这里介绍用组合数性质求解:注意到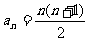 =
=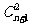 ,
,
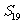 =
=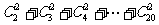 =
=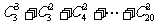 =
=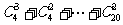 =
=
…=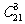 =1330;
=1330;
[巩固1]设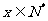 且
且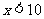 ,则
,则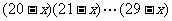 等于 ( )
等于 ( )
(A)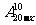 (B)
(B)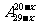 (C)
(C)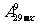 (D)
(D)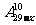
[巩固2] 已知 的展开式中第9项、第10项、第11项的二项式系数成等差数列,则n=____
的展开式中第9项、第10项、第11项的二项式系数成等差数列,则n=____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com