
20.(本小题满分12分)
已知点(1,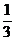 )是函数
)是函数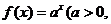 且
且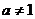 )的图象上一点,等比数列
)的图象上一点,等比数列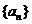 的前
的前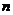 项和为
项和为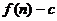 ,数列
,数列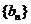
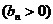 的首项为
的首项为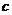 ,且前
,且前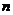 项和
项和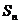 满足
满足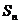 -
-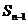 =
=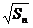 +
+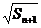 (
( ).
).
(1)求数列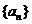 和
和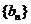 的通项公式;
的通项公式;
(2)若数列{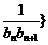 前
前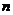 项和为
项和为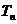 ,问
,问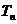 >
>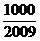 的最小正整数
的最小正整数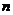 是多少?
是多少?
19.(本小题满分12分)
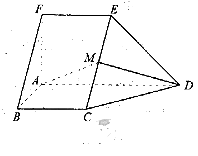 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 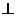 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB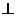 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=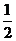 AD
AD
(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD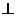 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
18.(本小题满分12分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是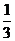 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间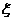 的分布列及期望.
的分布列及期望.
17.(本小题满分10分)
已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量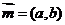 ,
,
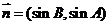 ,
,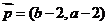 .(1)若
.(1)若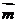 //
//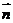 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)若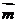 ⊥
⊥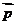 ,边长c = 2,角C =
,边长c = 2,角C = 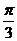 ,求ΔABC的面积
.
,求ΔABC的面积
.
16.已知函数f(x)=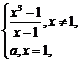 若f(x)在R上连续,则
若f(x)在R上连续,则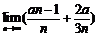 =___________.
=___________.
15.一个总体分为A,B两层,其个体数之比为4:1,用分层抽样方法从总体中抽取一个容量为10的样本,已知B层中甲、乙都被抽到的概率为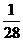 ,则总体中的个数为 。
,则总体中的个数为 。
14.设x、y满足约束条件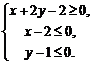 则z=x-y的最大值是_________.
则z=x-y的最大值是_________.
13.  的展开式中,
的展开式中,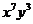 的系数与
的系数与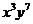 的系数之和等于 。
的系数之和等于 。
12.若三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,AB=2,SA=SB=SC=2,则该三棱锥的外接球的球心到平面ABC的距离为 ( )
A.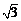 B.
B.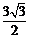 C.1 D.
C.1 D. 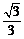
第Ⅱ卷(非选择题,共90分)
9.设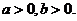 若
若 的最小值为
( )
的最小值为
( )
A 8
B 4 C
1 D 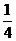
10设曲线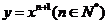 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为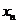 ,则
,则 的值为
(
)
的值为
(
)
(A) 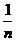 (B)
(B)
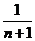 (C)
(C)
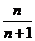 (D)
1
(D)
1
11从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有( )
A.120种 B96种 C.60种 D.48种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com