5．⑴A恰未滑离B板，则A达B最左端时具有相同速度v，有 Mv₀-mv₀=(M+m)v　 ∴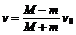

M＞m, ∴ v＞0,即与B板原速同向。

⑵A的速度减为零时，离出发点最远，设A的初速为v₀，A、B摩擦力为f，向左运动对地最远位移为S，则

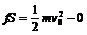　 　而v₀最大应满足 Mv₀-mv₀=(M+m)v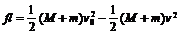　 　

　 解得：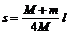

14. (1)以地面为参考系，小车与木板相向运动，共运动L=12 m.在木板对小车的摩擦力作用下小车做匀加速运动，加速度a₁=4 m/s²，F=ma₁=20 N，设木板向左的加速度为a₂，木板受小车的摩擦力F′等于小车受木板的摩擦力F，木板还受地面的摩擦力作用，F′-μ(m+M)g=Ma₂，代入数据解得：a₂=2 m/s²(2分)

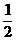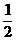再由距离关系：a₁t²+a₂t²=L，所以得到：t=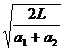=2 s.(4分)

(2)小车与弹簧夹碰撞前的速度方向向右v₁=a₁t=8 m/s，木板此时的速度方向向左，v₂=a₂t=4 m/s，木板向左的位移s=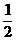a₂t²=4 m.(2分)

小车与弹簧夹碰撞过程中系统动量守恒：mv₁-Mv₂=(m+M)v_共，v_共=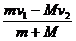=2 m/s，此后小车和木板一起向右滑行，设木板向右移动s′停止，则-μ(m+M)gs′=0-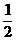(m+M)v_共²，s′=2 m，(2分)

木板移动的总位移：s_总=s-s′＝2 m，方向向左.(2分)

4金属块在板上滑动过程中，统动量守恒。金属块最终停在什么位置要进行判断。假设金属块最终停在A上。三者有相同速度v，相对位移为x，则有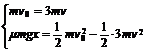　 解得：，因此假定不合理，金属块一定会滑上B。

设x为金属块相对B的位移，v₁、v₂表示A、B最后的速度，v₀′为金属块离开A滑上B瞬间的速度。有：在A上　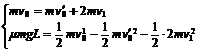 　全过程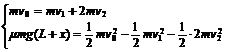

联立解得：　 ∴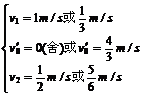

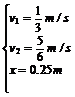
*解中，整个物理过程可分为金属块分别在A、B上滑动两个子过程，对应的子系统为整体和金属块与B。可分开列式，也可采用子过程→全过程列式，实际上是整体→部分隔离法的一种变化。

2.解:(1)因为小车与墙第一次相碰以后向左运动的过程中动量守恒,

取向右的方向为正,得:mv-Mv=(M+m) v₁　

因为 mv>Mv ,所以v₁>0,即系统的共同速度仍向右,因此还会与墙发生碰撞,这样反复碰撞直至能量消耗殆尽.

车与墙碰后,车跟物块发生相对滑动,以车为研究对象,由牛顿第二定律有: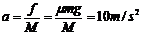.设车与墙第n次碰撞后的速度为v_n,碰后的共同速度为v_n+1,那么v_n+1也就是第n+1次碰撞后的速度,对系统应用动量守恒定律有:

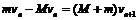,所以.

设车第n次与墙相碰后离墙的最大位移为s,则.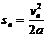

而.

则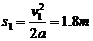,由此可知,车每次碰后与墙的最大位移成等比数列,公比为1/9,所以小车与墙第一次相碰后所走的总路程为:

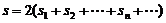
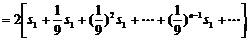
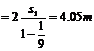
(2)对物块和平板车组成的系统,在整个过程中由能的转化和守恒定律得:

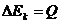,即.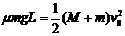

则平板车的最小长度为: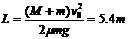

8．一质量为m、两端有挡板的小车静止在光滑水平面上，两挡板间距离为1.1m，在小车正中放一质量为m、长度为0.1m的物块，物块与小车间动摩擦因数μ=0.15。如图示。现给物块一个水平向右的瞬时冲量，使物块获得v₀ =6m/s的水平初速度。物块与挡板碰撞时间极短且无能量损失。求：

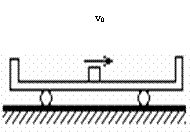⑴小车获得的最终速度；

⑵物块相对小车滑行的路程；

⑶物块与两挡板最多碰撞了多少次；

⑷物块最终停在小车上的位置。

7．在光滑水平面上静止放置一长木板B，B的质量为M=2㎏同，B右端距竖直墙5m，现有一小物块 A，质量为m=1㎏，以v₀=6m/s的速度从B左端水平地滑上B。如图所示。A、B间动摩擦因数为μ=0.4，B与墙壁碰撞时间极短，且碰撞时无能量损失。取g=10m/s²。求：要使物块A最终不脱离B

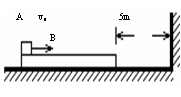木板，木板B的最短长度是多少？

6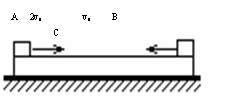．一平直木板C静止在光滑水平面上，今有两小物块A和B分别以2v₀和v₀的初速度沿同一直线从长木板C两端相向水平地滑上长木板。如图示。设物块A、B与长木板

C间的动摩擦因数为μ，A、B、C三者质量相等。

⑴若A、B两物块不发生碰撞，则由开始滑上C到A、B都静止在

C上为止，B通过的总路程多大？经历的时间多长？

⑵为使A、B两物块不发生碰撞，长木板C至少多长？

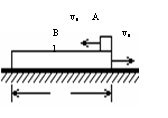
5．如图示，一质量为M长为l的长方形木块B放在光滑水平面上，在其右端放一质量为m的小木块A，m＜M，现以地面为参照物，给A和B以大小相等、方向相反的初速度(如图)，使A开始向左运动，B开始向右运动，但最后A刚好没有滑离B板。以地面为参照系。

⑴若已知A和B的初速度大小为v₀，求它们最后速度的大小和方向；

⑵若初速度的大小未知，求小木块A向左运动到最远处(从地面上看)到出发点的距离。

4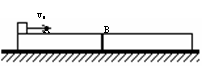．在光滑水平面上并排放两个相同的木板，长度均为L=1.00m，一质量

与木板相同的金属块，以v₀=2.00m/s的初速度向右滑上木板A，金属

块与木板间动摩擦因数为μ=0.1，g取10m/s²。求两木板的最后速度。

3. (12分)如图所示,长L=12 m、右端有一弹簧夹的木板,质量M=5 kg,放在水平地面上,木板与地面间的动摩擦因数为0.1,质量m=5 kg的电动小车(可视为质点)位于木板的左端,小车启动后以4 m/s²的加速度匀加速向木板右端驶去,当小车撞击弹簧夹后被立即切断电源,且被弹簧夹子卡住.试求:

(1)小车从启动到被卡住所经历的时间.

(2)从小车启动到最终木板静止，木板的总位移.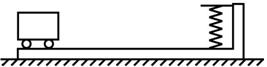

2、如图所示,质量为M=1kg的平板车左端放有质量为m=2kg的物块(看成质点),物块与车之间的动摩擦因数μ=0.5.开始时车和物块以v₀=6m/s的速度向右在光滑水平面上前进,并使车与墙发生正碰,设碰撞时间及短,且碰撞后车的速率与碰前的相等,车身足够长,使物块不能与墙相碰,取g=10m/s²,求:

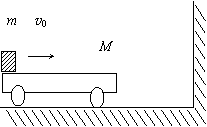(1)小车与墙第一次相碰以后小车所走的总路程.

(2)为使物块始终不会滑出平板车右端,平板车至少多长?