
22.(本小题满分14分)
设PQ是双曲线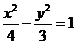 的余弦,且PQ与
的余弦,且PQ与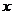 轴垂直,
轴垂直,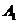 、
、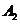 是双曲线的左、右顶点。
是双曲线的左、右顶点。
(1) 求直线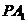 和
和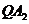 的焦点的轨迹C的方程;
的焦点的轨迹C的方程;
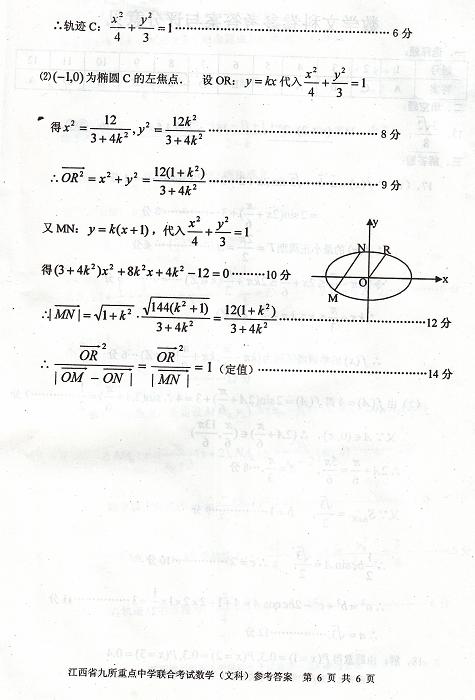
(2) 设直线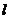 过点
过点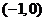 ,且与轨迹C相交于M、N两点,R为轨迹C上的一点,O为坐标原点,且
,且与轨迹C相交于M、N两点,R为轨迹C上的一点,O为坐标原点,且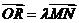 。问
。问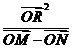 是否为定值?若是,求出该定值;若不是,请说明理由。
是否为定值?若是,求出该定值;若不是,请说明理由。

高1考1资1源2网
高1考1资1源2网
高1考1资1源2网

高1考1资1源2网

高1考1资1源2网
高1考1资1源2网
21.(本小题满分12分)
已知各项均为正数的数列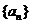 满足
满足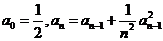 ,其中
,其中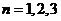
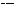 。
。
(1) 求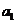 和
和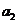 的值;
的值;
(2) 求证: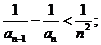
(3) 求证: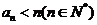 高1考1资1源2网
高1考1资1源2网
20.(本小题满分12分)
已知函数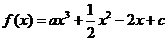
(1) 若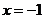 是
是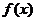 的极值点且
的极值点且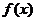 的图像过原点,求
的图像过原点,求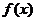 的极值;
的极值;
(2) 若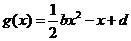 ,在(1)的条件下,是否存在实数
,在(1)的条件下,是否存在实数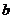 ,使得函数
,使得函数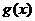 的图像与函数
的图像与函数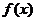 的图像恒有含
的图像恒有含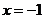 的三个不同交点?若存在,求出实数
的三个不同交点?若存在,求出实数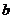 的取值范围;否则说明理由。高1考1资1源2网
的取值范围;否则说明理由。高1考1资1源2网
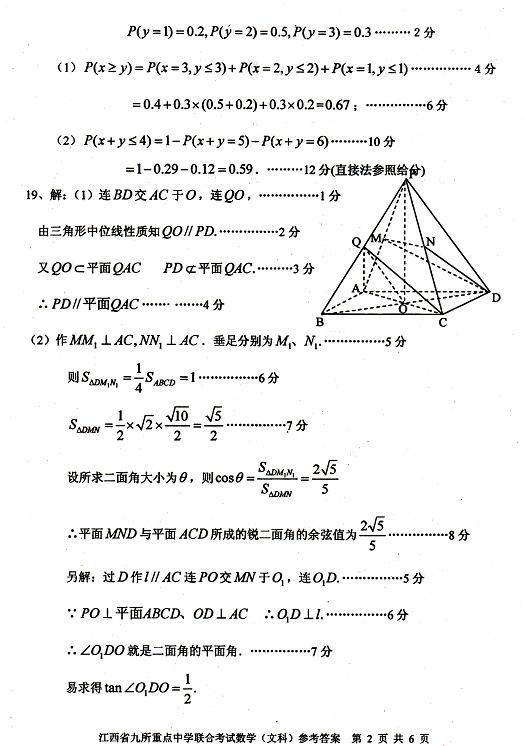
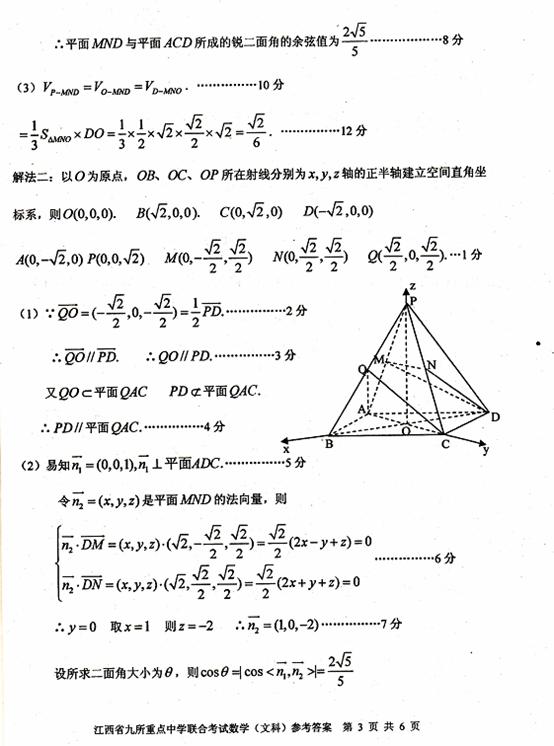
19.(本小题满分12分)
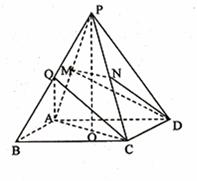
如图,正四棱锥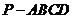 各棱长都为2,点
各棱长都为2,点
O、M、N、Q分别是AC、PA、PC、PB的中点。
(1)求证: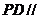 平面
平面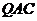 ;
;
(2)求平面MND与平面ACD所成的锐角二面角的余弦值
的大小;
(3) 求三棱锥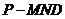 的体积。高1考1资1源2网
的体积。高1考1资1源2网
18.(本小题满分12分)
为适应新课程改革的需要,调动学生学习的兴趣,拓宽学生学习的视野,某中学对高二年级理科、文科分别开设了三门选修课,学生是否选修哪门课互不影响。经对高二理科、文科各随机抽取50人进行问卷调查,获得数据如下:高1考1资1源2网

若总体按此规律分布。
(1) 求理科所选门数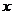 不少于文科所选门数
不少于文科所选门数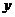 的概率;
的概率;
(2) 求事件“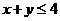 ”的概率。
”的概率。
17.(本小题满分12分)
已知向量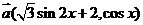 ,
,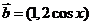 ,设函数
,设函数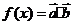 ,高1考1资1源2网
,高1考1资1源2网
(1) 求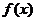 的最小正周期与单调增区间;
的最小正周期与单调增区间;
(2) 在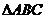 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为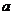 、
、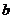 、
、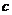 ,若
,若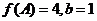 ,
,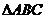 的面积为
的面积为 ,求
,求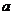 的值。高1考1资1源2网
的值。高1考1资1源2网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com