
2. “NaCl+CO2+NH3+H2O=NaHCO3↓+NH4Cl”是著名的“侯氏制碱法”的重要反应。下面是4位同学对该反应涉及的有关知识发表的部分见解。其中不正确的是(C)








A B C D
1.有甲、乙、丙、丁四种物质,在化学反应中的关系是:甲+乙→丙+丁(B)
A.若甲为盐酸,丁为水,则乙一定为碱
B.若甲为碳水化合物,乙为氧气,则该反应一定为氧化反应
C.若将10g甲和15g乙混合,充分反应后,则生成丙和丁的质量总和一定为25g
D.若甲、乙、丙、丁都是化合物,则该反应一定是复分解反应
(二) 为偶数,则
为偶数,则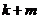 为偶数。则
为偶数。则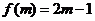 ,
,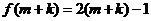 。则
。则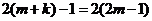 ,解得:
,解得: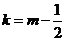 与
与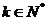 矛盾。 ----(1分)
矛盾。 ----(1分)
由此得:对于给定常数m( ),这样的
),这样的 总存在;当
总存在;当 是奇数时,
是奇数时,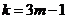 ;当
;当 是偶数时,
是偶数时,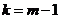 。
----(1分)
。
----(1分)
10.(2009南华一中12月月考)设各项均为正数的数列 的前
的前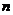 项和为
项和为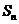 ,且满足:
,且满足: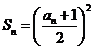
(1) 求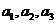 ;
;
(2)求出数列 的通项公式(写出推导过程);
的通项公式(写出推导过程);
(3) 设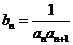 ,求数列
,求数列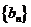 的前
的前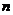 项和。
项和。
解:(1)由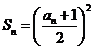 得
得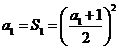 解得
解得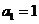 …………………1分
…………………1分
由 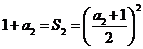 解得
解得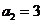 ……………………………………2分
……………………………………2分
由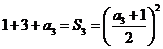 解得
解得 …………………………………3分
…………………………………3分
(2)当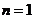 时
时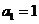
当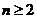 时,
时,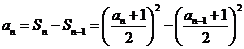 ……………4分
……………4分
整理得: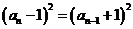
化简得: ………………………………………………………6分
………………………………………………………6分
所以 是公差为2,首项为1的等差数列,
是公差为2,首项为1的等差数列,
即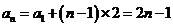 …………………………………………………7分
…………………………………………………7分
(3)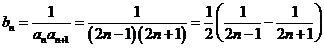 ………………9分
………………9分
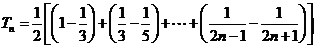
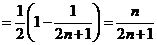 ………………………………………………12分
………………………………………………12分
11.(2009枣庄一模)设数列
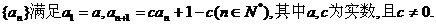
(1)求数列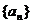 的通项公式;
的通项公式;
(2)设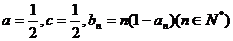 ,求数列
,求数列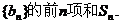
解:(1)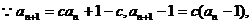
 是首项为
是首项为 的等比数列 2分
的等比数列 2分
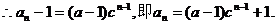 4分
4分
当 仍满足上式。
仍满足上式。
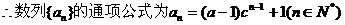
注:未考虑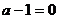 的情况,扣1分。
的情况,扣1分。
(2)由(1)得,当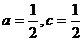 时,
时,
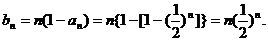 8分
8分

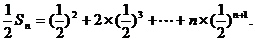
两式作差得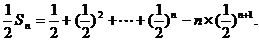
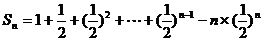
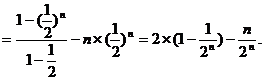
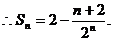 12分
12分
12.(2009冠龙高级中学3月月考)由函数 确定数列
确定数列 ,
, ,函数
,函数 的反函数
的反函数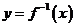 能确定数列
能确定数列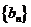 ,
, ,若对于任意
,若对于任意 ,都有
,都有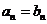 ,则称数列
,则称数列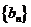 是数列
是数列 的“自反数列”。
的“自反数列”。
(1)若函数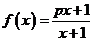 确定数列
确定数列 的自反数列为
的自反数列为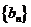 ,求
,求 的通项公式;
的通项公式;
(2)在(1)条件下,记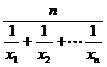 为正数数列
为正数数列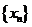 的调和平均数,若
的调和平均数,若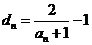 ,
,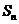 为数列
为数列 的前
的前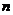 项和,
项和,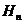 为数列
为数列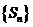 的调和平均数,求
的调和平均数,求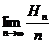 ;
;
(3)已知正数数列 的前
的前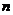 项之和
项之和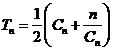 。求
。求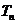 的表达式。
的表达式。
解:(1)由题意的:f –1(x)=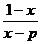 = f(x)=
= f(x)= ,所以p = –1,所以an=
,所以p = –1,所以an=
(2) an= ,dn=
,dn=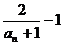 =n,
=n,
Sn为数列{dn}的前n项和,Sn= ,又Hn为数列{Sn}的调和平均数,
,又Hn为数列{Sn}的调和平均数,
Hn=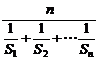 =
=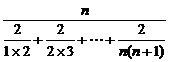 =
=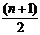
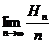 =
= =
=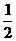
(3)因为正数数列{cn}的前n项之和Tn=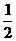 (cn+
(cn+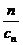 ),
),
所以c1=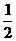 (c1+
(c1+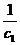 ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
当n≥2时,cn = Tn–Tn–1,所以2Tn = Tn–Tn–1 + ,
,
Tn +Tn–1 =  ,即:
,即: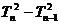 = n,
= n,
所以, = n–1,
= n–1,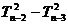 = n–2,……,
= n–2,……, =2,累加得:
=2,累加得:
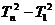 =2+3+4+……+ n,
=2+3+4+……+ n, 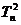 =1+2+3+4+……+ n =
=1+2+3+4+……+ n =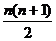 ,Tn=
,Tn=
13.(2009番禺一模)设数列 对一切正整数
对一切正整数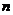 均有
均有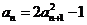 ,且
,且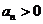 ,如果
,如果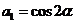 ,
,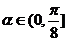 .
.
(1)求 ,
,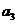 的值;
的值;
(2)求数列
 的通项公式;
的通项公式;
(3)设数列 前
前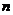 项之积为
项之积为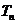 ,试比较
,试比较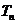 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
(1)依题意: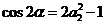 ,则
,则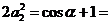 ,
,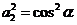
而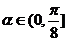 ,又
,又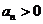 ,所以
,所以 ,
………………1分
,
………………1分
同样可求得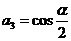 ,
………………2分
,
………………2分
(2)猜测 ,
,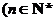 )
………………4分
)
………………4分
①用数学归纳法证明:显然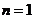 时猜想正确,
………………5分
时猜想正确,
………………5分
②假设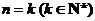 时猜想成立,即
时猜想成立,即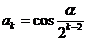 ,
,
则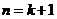 时,∵
时,∵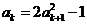 ,∴
,∴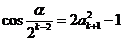 ,即
,即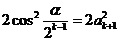 ,而
,而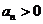
故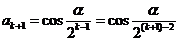 ,
………………6分
,
………………6分
这就是说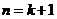 猜想也成立,故对任意正整数
猜想也成立,故对任意正整数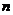 都有
都有 . ………………7分
. ………………7分
(3)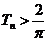 ……………9分
……………9分
证明: 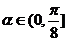 ,
,
则 ,
………10分
,
………10分
则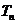
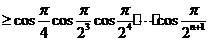
∴ ………11分
………11分
设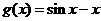 ,
,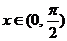 ,则
,则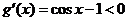 ,
,
即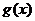 为
为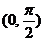 上的减函数,∴
上的减函数,∴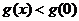 ,故
,故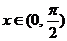 时,
时,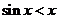 , ……12分
, ……12分
而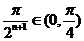 ,∴
,∴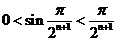 ,
,
∴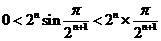 ………13分
………13分
∴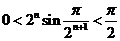 ,,
,,
则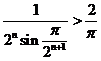 ,即
,即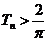 .
14分
.
14分
14.(2009深圳一模理)已知函数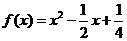 ,
,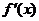 为函数
为函数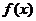 的导函数.
的导函数.
(Ⅰ)若数列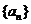 满足:
满足: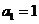 ,
,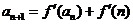 (
(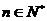 ),求数列
),求数列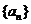 的通项
的通项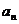 ;
;
(Ⅱ)若数列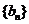 满足:
满足: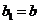 ,
,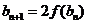 (
(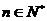 ).
).
(ⅰ)当 时,数列
时,数列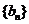 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列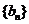 的通项
的通项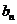 ;若不是,请说明理由;
;若不是,请说明理由;
(ⅱ)当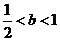 时, 求证:
时, 求证: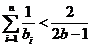 .
.
解:(Ⅰ)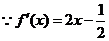 ,
…………………………1分
,
…………………………1分
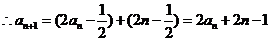 ,
,
即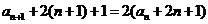 …………………………3分
…………………………3分
 ,
, 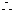 数列
数列 是首项为
是首项为 ,公比为
,公比为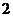 的等比数列.
的等比数列.
 ,即
,即
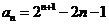 .
…………………………5分
.
…………………………5分
(Ⅱ)(ⅰ)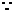
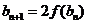
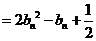 ,
,
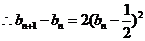 .
.
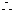 当
当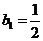 时,
时,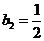 .
.
假设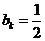 ,则
,则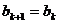 .
.
由数学归纳法,得出数列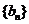 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为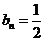 .…8分
.…8分
(ⅱ)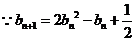 ,
,
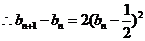 .
.
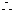 当
当 时,
时,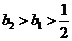 .
.
假设 ,则
,则
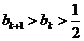 .
.
由数学归纳法,得出数列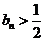
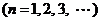 .……………10分
.……………10分
又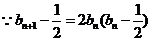 ,
,
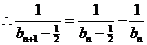 ,
,
即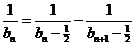 .
…………………………12分
.
…………………………12分
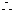
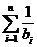
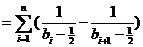
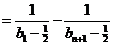 .
.
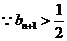 ,
,
 .
…………………………14分
.
…………………………14分
(一) 为奇数,则
为奇数,则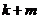 为奇数。则
为奇数。则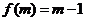 ,
, 。则
。则 ,解得:
,解得: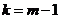 (
(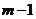 是正奇数)。
----(1分)
是正奇数)。
----(1分)
(二) 为偶数,则
为偶数,则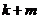 为奇数。则
为奇数。则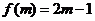 ,
, 。则
。则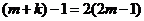 ,解得:
,解得: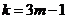 (
(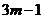 是正偶数)。 ----(1分)
是正偶数)。 ----(1分)
(B) 为偶数
为偶数
(一) 为奇数,则
为奇数,则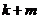 为偶数。则
为偶数。则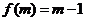 ,
,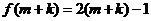 。则
。则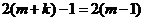 ,解得:
,解得: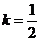 与
与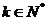 矛盾。
----(1分)
矛盾。
----(1分)
1.(2009上海卢湾区4月模考)已知数列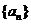 的前
的前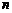 项和为
项和为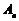 ,且对任意正整数
,且对任意正整数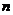 ,都满足:
,都满足: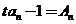 ,其中
,其中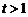 为实数.
为实数.
(1)求数列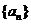 的通项公式;
的通项公式;
(2)若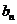 为杨辉三角第
为杨辉三角第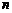 行中所有数的和,即
行中所有数的和,即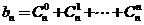 ,
,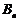 为杨辉三角前
为杨辉三角前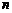 行中所有数的和,亦即为数列
行中所有数的和,亦即为数列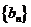 的前
的前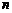 项和,求
项和,求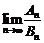 的值.
的值.
解:(1) 由已知 ,
,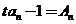 ,相减得
,相减得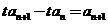 ,由
,由 得
得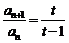 ,又
,又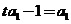 ,得
,得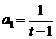 ,故数列
,故数列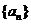 是一个以
是一个以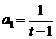 为首项,以
为首项,以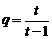 为公比的等比数列.
(4分)
为公比的等比数列.
(4分)
从而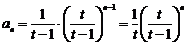
 ;
(6分)
;
(6分)
(2)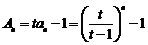 ,
(7分)
,
(7分)
又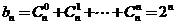 ,故
,故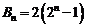 ,
(11分)
,
(11分)
于是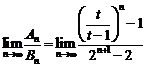 ,
,
当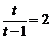 ,即
,即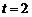 时,
时,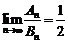 ,
,
当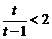 ,即
,即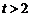 时,
时,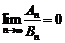 ,
,
当 ,即
,即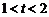 时,
时,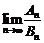 不存在.
(14分)
不存在.
(14分)
2.(2009临沂一模)已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(I) 求数列{an}的通项公式;
(II)
若bn=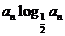 ,sn=b1+b2+┉+bn,求sn+n•
,sn=b1+b2+┉+bn,求sn+n•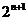 >50成立的正整数 n的最小值。
>50成立的正整数 n的最小值。
解:(I)设等比数列{an}的首项为a1,公比为q,
依题意,有2(a3+2)=a2+a4,
代入a2+a3+a4=28, 得a3=8,
∴a2+a4=20┉┉┉┉┉┉┉┉2分
∴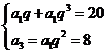 解之得
解之得 或
或 ┉┉┉┉┉┉┉┉4分
┉┉┉┉┉┉┉┉4分
又{an}单调递增,∴q=2,a1=2,
∴an=2n ┉┉┉┉┉┉┉┉6分
(II)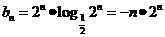 ,
┉┉┉┉┉┉┉┉7分
,
┉┉┉┉┉┉┉┉7分
∴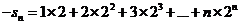 ①
①
∴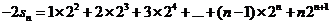 ②
②
∴①-②得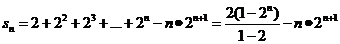 =
=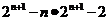 ┉10分
┉10分
∴ 即
即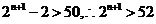
又当n≤4时,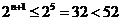 ,
┉┉┉┉┉┉┉┉11分
,
┉┉┉┉┉┉┉┉11分
当n≥5时, .
.
故使 成立的正整数n的最小值为5
. ┉┉┉┉┉┉┉┉12分
成立的正整数n的最小值为5
. ┉┉┉┉┉┉┉┉12分
3.(2009杭州高中第六次月考)已知数列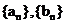 中,
中,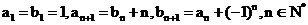
(1)求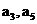 的值;
的值;
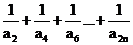 (2)求证:
(2)求证:
(3)求 的值.
(1) 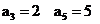 ------------------------4分
------------------------4分
(2)由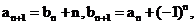 可得
可得
 ------------------------6分
------------------------6分
所以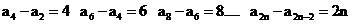 ------------------------8分
------------------------8分
将上述式子相加得 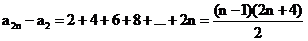

 (或者用数学归纳法证明)------------------------10分
(或者用数学归纳法证明)------------------------10分
(3)
4.(2009青岛一模)已知等比数列 的前
的前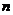 项和为
项和为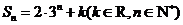
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列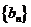 满足
满足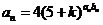 ,
,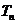 为数列
为数列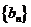 的前
的前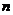 项和,试比较
项和,试比较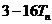 与
与 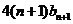 的大小,并证明你的结论.
的大小,并证明你的结论.
解:(Ⅰ)由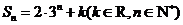 得:
得: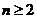 时,
时,
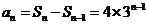 ………………………2分
………………………2分
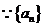 是等比数列,
是等比数列,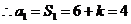
 ,得
,得  ……4分
……4分
(Ⅱ)由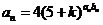 和
和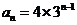 得
得 ……………………6分
……………………6分
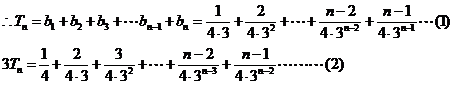

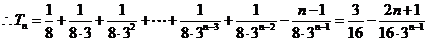 ……10分
……10分
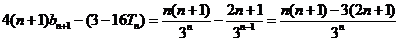
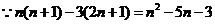 ………………………11分
………………………11分
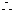 当
当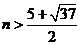 或
或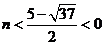 时有
时有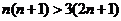 ,所以当
,所以当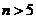
 时有
时有
那么同理可得:当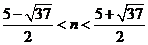 时有
时有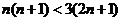 ,所以当
,所以当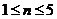
 时有
时有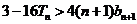 ………………………13分
………………………13分
综上:当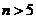
 时有
时有 ;当
;当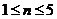
 时有
时有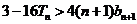 ………………………14分
………………………14分
5.(2009日照一模)已知数列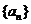 的各项均为正数,
的各项均为正数,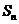 为其前
为其前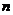 项和,对于任意的
项和,对于任意的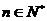 ,满足关系式
,满足关系式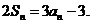
(I)求数列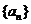 的通项公式;
的通项公式;
(Ⅱ)设数列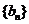 的通项公式是
的通项公式是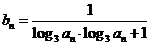 ,前
,前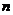 项和为
项和为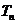 ,求证:对于任意的正整数
,求证:对于任意的正整数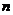 ,总有
,总有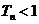
解:(I)由已知得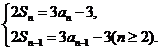
故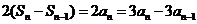
即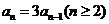
故数列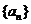 为等比数列,且
为等比数列,且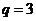
又当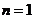 时,
时,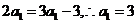
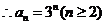 ………………………………6分
………………………………6分
而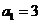 亦适合上式
亦适合上式
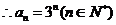 …………………………………8分
…………………………………8分
(Ⅱ)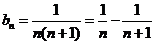
所以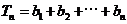
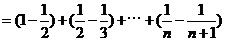
 ………………………………12分
………………………………12分
6.(2009昆明市期末)数列{an}的前n项和为Sn,且a1=a,Sn+1=2Sn+n+1,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)当a=1时,若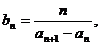 设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
(Ⅰ)由Sn+1=2Sn+n+1 ①得
①得
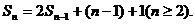 ②
②
①-②得
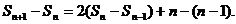
故 an+1=2an +1。(n≥2)··································(2分)
又 an+1+1=2(an+1),
所以 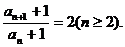
故数列{an+1}是从第2项其,以a2+1为首项,公比为2的等比数列。
又 S2=2S1+1+1,a1=a,所以a2=a+2。
故 an=(a+3)·2n-2-1(n≥2).
又a1=a不满足an=(a+3)·2n-2-1,
所以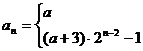
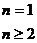 ····································6分
····································6分
(Ⅱ)由a1=1,得an==2n-1,n∈N*,则
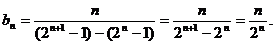
又 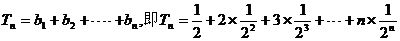 ①
①
得 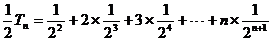 ②
②
①-②得

故 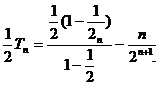
所以 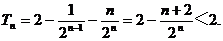 ································12分
································12分
7.(2009东莞一模)设等差数列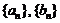 前
前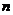 项和
项和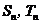 满足
满足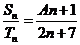 ,且
,且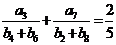 ,S2=6;函数
,S2=6;函数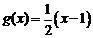 ,且
,且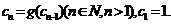
(1)求A;
(2)求数列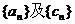 的通项公式;
的通项公式;
(3)若
解:(1)由 而
而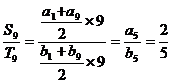
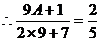 解得A=1……………………………………2分
解得A=1……………………………………2分
(2)令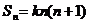
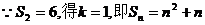
当n=1时,a1=S1=2,当n≥2时,an=Sn-Sn-1=n2+n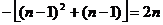
综合之:an=2n…………………………………………6分
由题意
∴数列{cn+1}是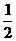 为公比,以
为公比,以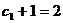 为首项的等比数列。
为首项的等比数列。
 ………………………9分
………………………9分
(3)当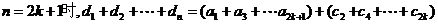
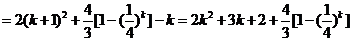
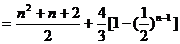 ………………………11分
………………………11分
当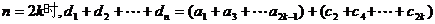
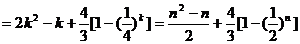 ………13分
………13分
综合之:
………14分
8.(2009泰安一模)已知数列{a }中,
}中, ,点
,点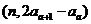 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(I)
令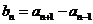 ,求证数列{b
,求证数列{b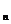 }是等比数列;
}是等比数列;
(II)
球数列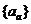 的通项
的通项
解:(I)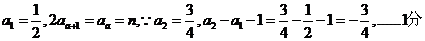
又
9.(2009上海奉贤区模拟考)已知点集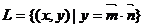 ,其中
,其中 ,
, ,点列
,点列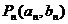 在L中,
在L中, 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列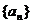 的公差为1,
的公差为1,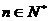 。
。
(1)求数列 的通项公式;
的通项公式;
(2)若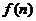 =
= ,令
,令 ;试用解析式写出
;试用解析式写出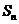 关于
关于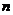 的函数。
的函数。
(3)若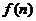 =
= ,给定常数m(
,给定常数m( ),是否存在
),是否存在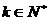 ,使得
,使得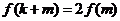 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(1)y= ·
· =(2x-b)+(b+1)=2x+1
-----(1分)
=(2x-b)+(b+1)=2x+1
-----(1分)
 与
与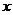 轴的交点
轴的交点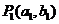 为
为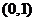 ,所以
,所以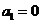 ;
-----(1分)
;
-----(1分)
所以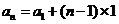 ,即
,即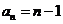 ,
-----(1分)
,
-----(1分)
因为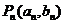 在
在 上,所以
上,所以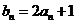 ,即
,即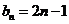 -----(1分)
-----(1分)
(2)设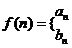
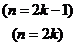 (
(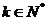 ),
),
即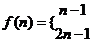
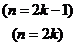 (
(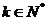 ) ----(1分)
) ----(1分)
(A)当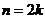 时,
时,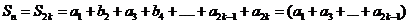
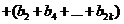 ----(1分)
----(1分)
=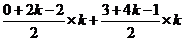 =
=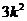 ,而
,而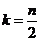 ,所以
,所以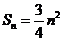 ----(1分)
----(1分)
(B)当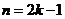 时,
时,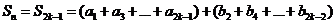 ----(1分)
----(1分)
= 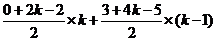 =
= ,
----(1分)
,
----(1分)
而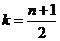 ,所以
,所以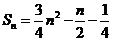 ----(1分)
----(1分)
因此 (
(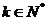 )
----(1分)
)
----(1分)
(3)假设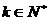 ,使得
,使得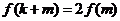 ,
,
(A) 为奇数
为奇数
5. (2009金华一中2月月考)将正奇数排列如下表其中第
(2009金华一中2月月考)将正奇数排列如下表其中第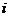 行第
行第 个数表示
个数表示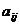
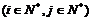 ,例如
,例如
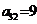 ,若
,若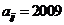 ,则
,则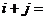 .
.
答案 60
4. (2009上海九校联考)已知数列 的前
的前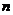 项和为
项和为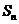 ,若
,若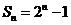 ,则
,则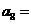 .
.
答案 128
3.(2009闵行三中模拟)已知 是等比数列,
是等比数列,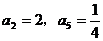 ,则
,则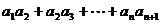 = 。
= 。
答案 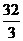 (
(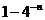 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com