
22.(本题满分14分)
在平面直角坐标系中,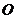 为坐标原点,已知两点
为坐标原点,已知两点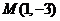 、
、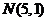 ,若动点
,若动点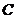 满足
满足 且点
且点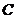 的轨迹与抛物线
的轨迹与抛物线 交于
交于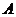 、
、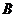 两点.
两点.
(Ⅰ)求证: ;
;
(Ⅱ)在 轴上是否存在一点
轴上是否存在一点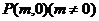 ,使得过点
,使得过点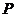 的直线
的直线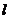 交抛物线
交抛物线 于于
于于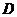 、
、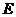 两点,并以线段
两点,并以线段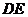 为直径的圆都过原点。若存在,请求出
为直径的圆都过原点。若存在,请求出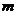 的值及圆心
的值及圆心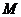 的轨迹方程;若不存在,请说明理由.
的轨迹方程;若不存在,请说明理由.
2009-2010学年度第一学期第二学段学情自主测评
21.(本题满分12分)
已知函数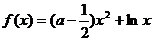 .(
.( )
)
(Ⅰ)当 时,求
时,求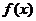 在区间
在区间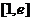 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间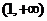 上,函数
上,函数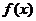 的图象恒在直线
的图象恒在直线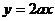 下方,求
下方,求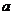 的取值范围.
的取值范围.
20.(本题满分12分)
已知点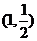 是函数
是函数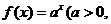 且
且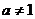 )的图象上一点,等比数列
)的图象上一点,等比数列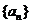 的前
的前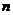 项和为
项和为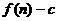 ,数列
,数列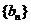
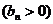 的首项为
的首项为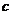 ,且前
,且前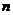 项和
项和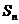 满足
满足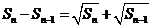 (
(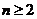 ).
).
(Ⅰ)求数列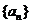 和
和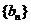 的通项公式;
的通项公式;
(Ⅱ)若数列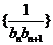 前
前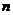 项和为
项和为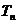 ,问满足
,问满足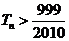 的最小正整数
的最小正整数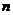 是多少?
是多少?
19.(本题满分12分)
如图正三棱柱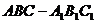 ,
,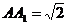 ,
,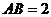 ,若
,若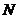 为棱
为棱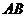 中点.
中点.
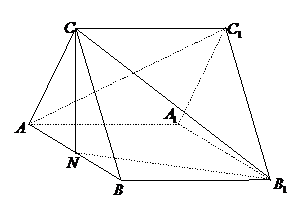 (Ⅰ)求证:
(Ⅰ)求证: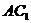 ∥平面
∥平面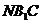 ;
;
(Ⅱ)求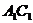 与平面
与平面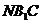 所成的角正弦值.
所成的角正弦值.
18.(本题满分12分)
某商场为刺激消费,拟按以下方案进行促销:顾客每消费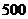 元便得到抽奖券一张,每张抽奖券的中奖概率为
元便得到抽奖券一张,每张抽奖券的中奖概率为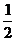 ,若中奖,商场返回顾客现金
,若中奖,商场返回顾客现金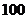 元.某顾客现购买价格为
元.某顾客现购买价格为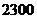 元的台式电脑一台,得到奖券
元的台式电脑一台,得到奖券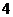 张.
张.
(Ⅰ)设该顾客抽奖后中奖的抽奖券张数为 ,求
,求 的分布列;
的分布列;
(Ⅱ)设该顾客购买台式电脑的实际支出为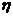 (元),用
(元),用 表示
表示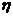 ,并求
,并求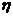 的数学期望.
的数学期望.
17.(本题满分12分)
已知函数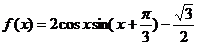 .
.
(Ⅰ)求函数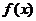 的最小正周期;
的最小正周期;
(Ⅱ)在给定的坐标系内,用五点
作图法画出函数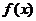 在一个周期内的
在一个周期内的
图象.
16.在实数的原有运算法则中,定义新运算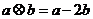 ,则
,则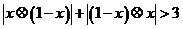
的解集为 .
15.已知两个不同的平面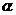 、
、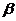 和两条不重合的直线
和两条不重合的直线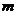 、
、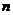 ,给出下列四个命题:
,给出下列四个命题:
①若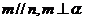 ,则
,则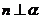 ;
②若
;
②若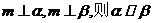 ;
;
③若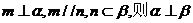 ; ④若
; ④若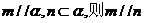 .
.
其中正确命题的序号是 .(写出所有正确命题的序号)
14.若双曲线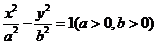 的两个焦点为
的两个焦点为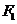 ,
,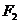 ,
,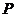 为双曲线上一点,且
为双曲线上一点,且
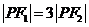 ,则该双曲线离心率的取值范围是 .
,则该双曲线离心率的取值范围是 .
13.已知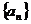 是等差数列,
是等差数列, ,
,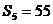 ,则过点
,则过点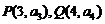 的直线的斜率是
的直线的斜率是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com