
21.(本题满分14分)
|
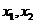 (
( )是方程
)是方程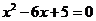 的两根,且
的两根,且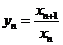 ,
,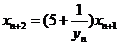 .
.
(1)求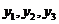 的值;
的值;
(2)设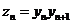 ,求证:
,求证: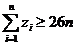 ;
;
(3)求证:对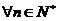 有
有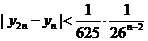 .
.
揭阳市2010年高中毕业班第一次高考模拟考
20.(本题满分14分)
设函数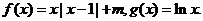

(1)当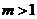 时,求函数
时,求函数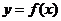 在
在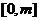 上的最大值;
上的最大值;
(2)记函数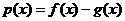 ,若函数
,若函数 有零点,求
有零点,求 的取值范围.
的取值范围.
19.(本题满分14分)
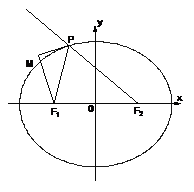
已知如图,椭圆方程为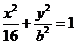
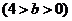 .P为椭圆上的动点,
.P为椭圆上的动点,
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;
(2)已知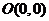 、
、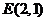 ,试探究是否存在这样的点
,试探究是否存在这样的点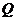 :
: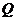 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积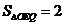 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
18.(本题满分14分)
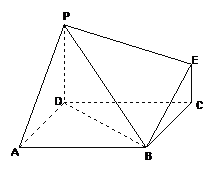
右图为一简单组合体,其底面ABCD为正方形,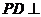 平面
平面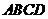 ,
,
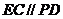 ,且
,且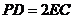 ,
,
(1)求证:BE//平面PDA;
(2)若N为线段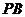 的中点,求证:
的中点,求证: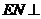 平面
平面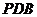 ;
;
 (3)若
(3)若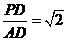 ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小.
17.(本题满分12分)
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元. 用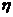 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.
(1)求上表中的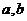 值;
值;
 (2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率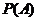 ;
;
(3)求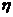 的分布列及数学期望
的分布列及数学期望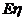 .
.
16.(本题满分12分)
已知复数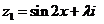 ,
,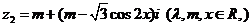 ,且
,且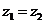 .
.
(1)若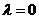 且
且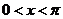
 ,求
,求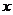 的值;
的值;
(2)设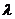 =
=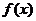 ,已知当
,已知当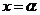 时,
时,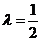 ,试求
,试求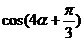 的值.
的值.
|
付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
频 数 |
40 |
20 |
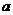 |
10 |
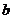 |
(二)选做题(14、15题,考生只能从中选做一题)
14. (坐标系与参数方程选做题) 设直线
(坐标系与参数方程选做题) 设直线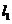 的参数方程为
的参数方程为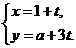 (
(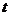 为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线
为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线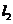 的方程为
的方程为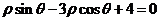 ,
,
若直线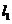 与
与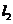 间的距离为
间的距离为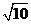 ,则实数
,则实数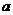 的值为
.
的值为
.
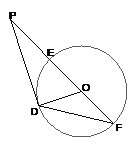
15.(几何证明选做题)如图,已知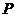 是
是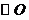 外一点,
外一点,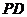 为
为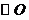 的切线,
的切线,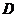 为
为
切点,割线PEF经过圆心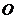 ,若
,若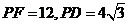 ,则
,则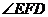 的度数为 .
的度数为 .
(一)必做题(9-13题)
9. 已知函数
已知函数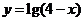 的定义域为
的定义域为 ,集合
,集合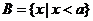 ,若P:“
,若P:“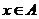 ”是
”是
Q:“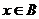 ”的充分不必要条件,则实数
”的充分不必要条件,则实数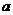 的取值范围 .
的取值范围 .
10.双曲线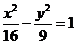 上一点P到右焦点的距离是实轴两端点到右焦
上一点P到右焦点的距离是实轴两端点到右焦
点距离的等差中项,则P点到左焦点的距离为 .
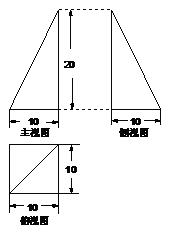
11.某师傅用铁皮制作一封闭的工件,其直观图的三视图如右图示
(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的
铁皮的面积为 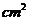 .(制作过程铁皮的损耗和厚度忽略不计)
.(制作过程铁皮的损耗和厚度忽略不计)
12.已知函数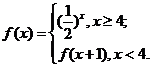 则
则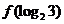 =
.
=
.
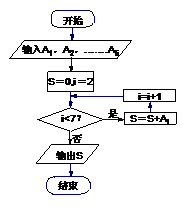
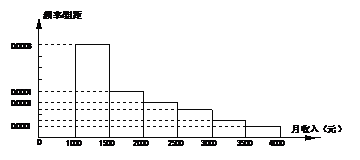
13.下图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图,
已知图甲中从左向右第一组的频数为4000. 在样本中记月收入在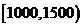 ,
,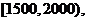
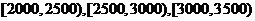 ,
,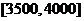 的人数依次为
的人数依次为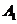 、
、 、……、
、……、 .图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,则样本的容量
.图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,则样本的容量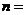 ;图乙输出的
;图乙输出的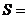 .(用数字作答)
.(用数字作答)
图甲 图乙
8.平面内称横坐标为整数的点为“次整点”.过函数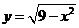 图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.
图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.
A.10 B.11 C.12 D.13
7.一物体A以速度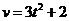 (
(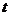 的单位:s,
的单位:s, 的单位:m/s),在一直线上运动,在此直线
的单位:m/s),在一直线上运动,在此直线
上在物体A出发的同时,物体B在物体A的正前方8m处以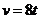 (
(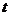 的单位:s,
的单位:s, 的单
的单
位:m/s)的速度与A同向运动,设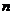 s后两物体相遇,则
s后两物体相遇,则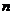 的值为
的值为
A.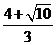 B.
B.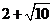 C.4 D.5
C.4 D.5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com