
20.(本小题满分12分)
数列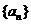 中,
中,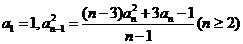 ,当
,当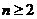 时,
时,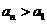 。
。
(1)求数列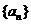 的通项公式;k+s-5?u
的通项公式;k+s-5?u
(2)若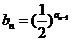 ,
,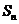 为数列
为数列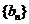 的前n项和,试比较
的前n项和,试比较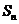 与
与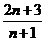 的大小。
的大小。
19. (本小题满分12分)
(本小题满分12分)
如图,正四棱锥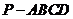 各棱长都为2,点O、M、N、Q分别是
各棱长都为2,点O、M、N、Q分别是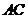 、
、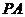 、
、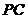 、
、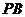 的中点。
的中点。
(1)求证:PD//平面QAC;
(2)求平面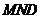 与平面
与平面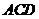 所成的锐二面角的大小;
所成的锐二面角的大小;
(3)求三棱锥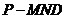 的体积。
的体积。
18.(本小题满分12分)
为适应新课程改革的需要,调动学生学习的兴趣,拓宽学生学习的视野,某中学对高二年级理科、文科分别开设了三门选修课,学生是否选修哪门课互不影响。经对高二理科、文科各随机抽取50人进行问卷调查,获得数据如下:
|
|
理科(人) |
文科(人) |
|
选修1门 |
15 |
10 |
|
选修2门 |
15 |
25 |
|
选修3门 |
20 |
15 |
若总体按此规律分布。
(1)求理科所选门数 不少于文科所选门数
不少于文科所选门数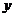 的概率;
的概率;
(2)记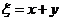 ,求
,求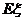 。
。
17.(本小题满分12分)
在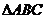 中,角
中,角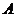 、
、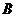 、
、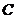 所对的边分别为
所对的边分别为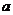 、
、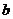 、
、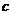 ,已知:
,已知: ,
, ,且
,且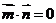 。
。
(1)求角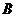 的大小;
的大小;
(2)若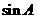 、
、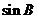 、
、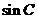 成等差数列,且
成等差数列,且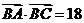 ,求
,求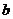 的值。
的值。
16.已知圆系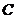 :
: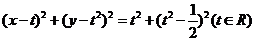 ,
,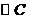 过
过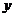 轴上的定点
轴上的定点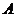 ,线段
,线段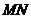 是
是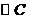 在
在 轴上截得的弦,设
轴上截得的弦,设 。对于下列命题:
。对于下列命题:
①不论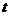 取何实数,圆心
取何实数,圆心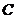 始终落在曲线
始终落在曲线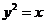 上;
上;
②不论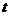 取何实数,弦
取何实数,弦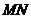 的长为定值1;k+s-5?u
的长为定值1;k+s-5?u
③不论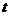 取何实数,圆系
取何实数,圆系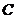 的所有圆都与直线
的所有圆都与直线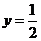 相切;
相切;
④式子 的取值范围是
的取值范围是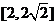 。
。
其中真命题的序号是 (把所有真命题的序号都填上)。
15.正四面体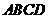 内接于球
内接于球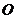 ,已知球
,已知球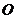 的体积为
的体积为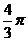 ,则
,则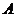 、
、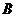 两点的球面距离为
。
两点的球面距离为
。
14.已知曲线 ,且
,且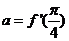 ,
,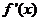 是
是 的导函数,则过曲线
的导函数,则过曲线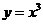 上一点
上一点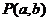 的切线方程为
。
的切线方程为
。
13. ,上式两边对
,上式两边对 求导后令
求导后令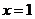 ,可得结论:
,可得结论: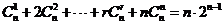 ,利用上述解题思路,可得到许多结论。试问:
,利用上述解题思路,可得到许多结论。试问: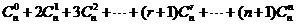 =
。
=
。
12.已知函数 的反函数为
的反函数为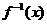 ,且
,且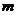 为函数
为函数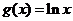 与函数
与函数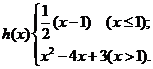 的交点个数,
的交点个数,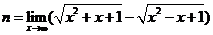 ,则函数
,则函数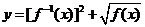 的值域是
的值域是
A.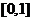 B.
B.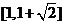 C.
C.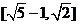 D.
D.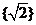
第II卷(非选择题 共90分)
11.设正四面体ABCD的所有棱长都为1米,有一只蚂蚁从点A开始按以下规则前进:在每一个顶点处等可能的选择通过这个顶点的三条棱之一,并且沿着这条棱爬到尽头,则它爬了4米之后恰好位于顶点A的概率为
A.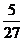 B.
B.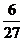 C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com