
10.解:(1)对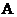 ,
, ,
,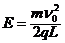 (2)
(2) 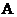 、
、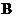 以
以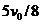 向右匀速运动,而
向右匀速运动,而 以初速度
以初速度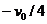 加速度
加速度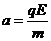 向右加速运动,设再次相遇有
向右加速运动,设再次相遇有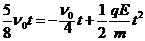 ,则
,则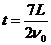 ,在这段时间内
,在这段时间内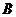 的位移
的位移 ,所以
,所以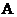 与
与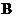 第二次相碰应发生在
第二次相碰应发生在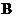 与
与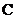 碰后(3)
碰后(3)
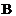 匀速运动
匀速运动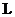 与
与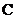 相碰时间
相碰时间 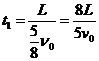 ,碰中:
,碰中: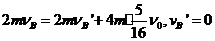 .w.w.^w.k.s.5* (2分)碰后
.w.w.^w.k.s.5* (2分)碰后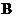 静止不动,而
静止不动,而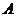 在电场力作用下加速,直至与
在电场力作用下加速,直至与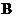 相碰,不难看出,在这段时间内
相碰,不难看出,在这段时间内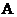 的位移为L,电场力做功
的位移为L,电场力做功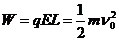
9.(20分)解答:设丙自然下落h时速度为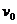 ,根据自由落体运动规律
,根据自由落体运动规律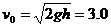 m/s①w.w.^w.k.s.5*
m/s①w.w.^w.k.s.5*
解除锁定后,乙与丙发生弹性碰撞,设碰后乙、丙的速度分别为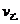 、
、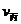 ,
,
根据动量守恒定律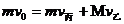 ② 2分根据动能守恒
② 2分根据动能守恒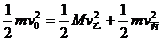 ③
③
 联立①②③解得
联立①②③解得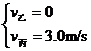 (舍去)
(舍去) ④
④
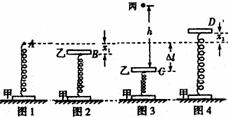
碰后,乙立即以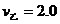 m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面的时间内,乙在自身重力和弹簧弹力的共同作用下以B点为平衡位置做简谐运动(如图)。
m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面的时间内,乙在自身重力和弹簧弹力的共同作用下以B点为平衡位置做简谐运动(如图)。
当乙第一次回到平衡位置B时,弹簧相对原长的压缩量(图2) ⑤ w.w.^w.k.s.5*
⑤ w.w.^w.k.s.5*
当甲第一次刚离开地面时,弹簧相对原长的伸长量(图4)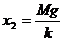 ⑥
⑥
由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和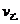 等大反向,所以根据简谐振动的对称性可知
等大反向,所以根据简谐振动的对称性可知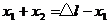 ⑦ 故
⑦ 故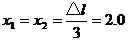 cm ⑧2分w.w.^w.k.s.5*
cm ⑧2分w.w.^w.k.s.5*
从碰撞结束至甲第一次刚离开地面时,对于乙核弹簧组成的系统,动能变化量为△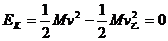 1分根据动能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹,△E弹=△E重 ⑨ 重力势能的增加量△重=Mg(x2+△l) ⑩
1分根据动能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹,△E弹=△E重 ⑨ 重力势能的增加量△重=Mg(x2+△l) ⑩
所以弹簧弹性势能的减少量为△E弹=Mg(x2+△l)=0.16J w.w.^w.k.s.5*
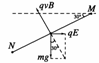
8.(12分)⑴球在MN段受力如图:
因为在MN段球做匀速直线运动,所以球受到如图所示的三个力而平衡
所以有:mgtan30° =qE,qvBsin30°=qE,联立解得:mg=3qE;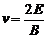 ;
;
(2)在x<0的区域内,设所加的电场强度为E′,则由运动情况分析知:
 球受的重力mg必与电场力qE′是一对平衡力,即:qE′=mg,∴ Eˊ = mg/q =
球受的重力mg必与电场力qE′是一对平衡力,即:qE′=mg,∴ Eˊ = mg/q =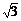 E
; E′的方向为竖直向上。(3)球在磁场中做匀速圆周运动的周期是: T=
E
; E′的方向为竖直向上。(3)球在磁场中做匀速圆周运动的周期是: T=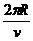 而:qvB=m
而:qvB=m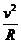 ∴ 在NP圆弧间经历的时间是:
∴ 在NP圆弧间经历的时间是:
7.(18分)解析:(1)设货物滑到圆轨道末端是的速度为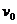 ,对货物的下滑过程中根据机械能守恒定律得,
,对货物的下滑过程中根据机械能守恒定律得, ① 设货物在轨道末端所受支持力的大小为
① 设货物在轨道末端所受支持力的大小为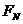 ,根据牛顿第二定律,
,根据牛顿第二定律,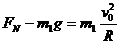 ② 代入数据得
② 代入数据得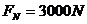 ③w.w.^w.k.s.5*
③w.w.^w.k.s.5*
根据牛顿第三定律,货物到达圆轨道末端时对轨道的压力大小为3000N,方向竖直向下 1分
(2)若滑上木板A时,木板不动,由受力分析得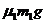 ≤
≤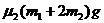 ④
④
若滑上木板B时,木板B开始滑动,由受力分析得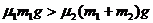 ⑤
⑤
联立④⑤式代入数据得0.4<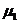 ≤0.6 ⑥w.w.^w.k.s.5*
≤0.6 ⑥w.w.^w.k.s.5*
(3)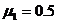 ,由⑥式可知,货物在模板A上滑动时,木板不动。
,由⑥式可知,货物在模板A上滑动时,木板不动。
设货物在木板A上做减速运动时的加速度大小为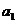 ,由牛顿第二定律得
,由牛顿第二定律得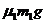 ≤
≤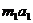 ⑦
⑦
设货物滑到木板A末端是的速度为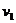 ,由运动学公式得
,由运动学公式得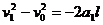 ⑧
⑧
 联立①⑦⑧式代入数据得
联立①⑦⑧式代入数据得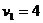 m/s ⑨设在木板A上运动的时间为t,由运动学公式得
m/s ⑨设在木板A上运动的时间为t,由运动学公式得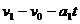 ⑩联立得
⑩联立得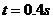
5. (12分)解:
(1)(4分)设路端电压为U,杆的运动速度为v,有
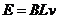 ,
, ,
,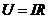
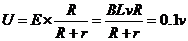
由图乙可得 U=0.2t
所以速度 v=2t
(2)(4分) 由v=2t知金属杆的加速度为2m/s2,在2s末,v=at=4m/s,
杆受安培力 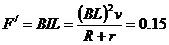 N
N
由牛顿第二定律,对杆有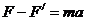 ,
,
得拉力F=0.35N
(3) (4分)在2s末, 杆的动能 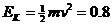 J
J
由能量守恒定律,回路产生的焦耳热 Q=W-Ek=0.4J
6解: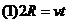 ,
,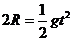 ,
,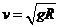 ,
,
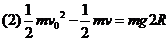 ,
,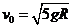 ,
,
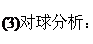
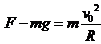 ,
,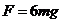 ,由牛顿第三定律可知:球对绳子的拉力为6mg,方向向下。(4)绳断时的速度为v1:
,由牛顿第三定律可知:球对绳子的拉力为6mg,方向向下。(4)绳断时的速度为v1: ,小球在最高点的速度v2 :
,小球在最高点的速度v2 : 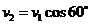
 。w.w.^w.k.s.5*
。w.w.^w.k.s.5*
3.(10分)解:(2分)(1)设电子经电压U1加速后的速度为v0,由动能定理
e U1=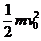 -0
-0
得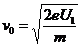
(2)(6分)电子以速度v0进入偏转电场后,垂直于电场方向做匀速直线运动,沿电场方向做初速度为零的匀加速直线运动。设偏转电场的电场强度为E,电子在偏转电场中运动的时间为t,加速度为a,电子离开偏转电场时的侧移量为y。由牛顿第二定律和运动学公式
t=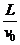
F=eE
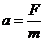
E=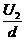
a =
y=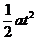
解得 y=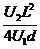
(3)(2分)减小加速电压U1;增大偏转电压U2。
(本题的答案不唯一,只要措施合理,答出一项即可得2分。)
4(12分)解:(1)(4分)a球恰能通过半圆环轨道最高点A时
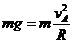
 a球从B运动到A过程中机械能守恒
a球从B运动到A过程中机械能守恒
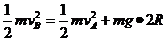
联立解得:

(2) (3分) b球则从桌面C点滑出做平抛运动
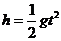
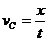 代入数据求得:
代入数据求得: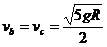
(3)(5分)以ab与弹簧为研究对象,动量守恒: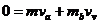
得: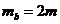
弹簧的弹性势能为:
得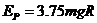
2.(10分)
解:(1)(4分) 设游客在山坡上滑行时加速度大小为a,游客滑到山坡底端时的速度大小为vB,则有:
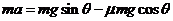
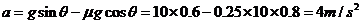
由
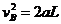
得: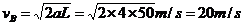
(2)(2分)此游客从A点到B点的下滑过程中摩擦力对他做的功:
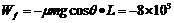 J
J
(3)(4分)设PB距离为x,游客在水平段滑行的加速度为
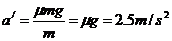
由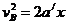 ,得
,得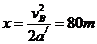
(另解:设PB距离为x,对全过程由动能定理得:
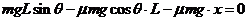
得: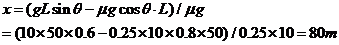 )
)
1.(10分)解:(1)(3分)小钢球从释放到落回星球表面做自由落体运动
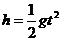 得
得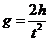
(2)(3分)钢球的重力等于万有引力
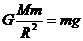 得此星球的质量为
得此星球的质量为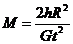
(3)(4分)距此星球表面高H的圆形轨道有一颗卫星绕它做匀速圆周运动,万有引力提供向心力
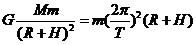 得
得
10.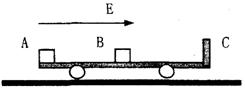 长为2L的板面光滑且不导电的平板车C放在光滑水平地面上,车的右端有一块挡板,车的质量为mC=4m,绝缘物体B的质量为mB=2m,B位于车板面的中间,带电的金属块A的质量mA=m,所带电荷量为+q.A、B开始处于图示位置而静止,今在整个空间加一水平向右的匀强电场,金属块A由静止开始向右运动,与B发生碰撞时的速度为v0,碰后A以v0/4的速度反弹回来,B向右运动(设A、B均可看作质点,且所有碰撞中无电荷量的转移,若B与C相碰,则碰后C的速度等于碰前B的速度的一半). (1) 求匀强电场场强的大小; (2) 若A第二次与B相碰,试通过计算判断是在B与C相碰之前还是相碰之后;(3)
A从第一次与B相碰到第二次与B相碰的过程中,电场力对A做了多少功.w.w.^w.k.s.5*
长为2L的板面光滑且不导电的平板车C放在光滑水平地面上,车的右端有一块挡板,车的质量为mC=4m,绝缘物体B的质量为mB=2m,B位于车板面的中间,带电的金属块A的质量mA=m,所带电荷量为+q.A、B开始处于图示位置而静止,今在整个空间加一水平向右的匀强电场,金属块A由静止开始向右运动,与B发生碰撞时的速度为v0,碰后A以v0/4的速度反弹回来,B向右运动(设A、B均可看作质点,且所有碰撞中无电荷量的转移,若B与C相碰,则碰后C的速度等于碰前B的速度的一半). (1) 求匀强电场场强的大小; (2) 若A第二次与B相碰,试通过计算判断是在B与C相碰之前还是相碰之后;(3)
A从第一次与B相碰到第二次与B相碰的过程中,电场力对A做了多少功.w.w.^w.k.s.5*
9. 直径轻弹簧的下端与水平地面上质量为M=0.20kg的甲木块连接,轻弹簧上端静止于A点(如图1),再将质量也为M=0.20kg乙木块与弹簧的上端连接,当甲、乙及弹簧均处于静止状态时,弹簧上端位于B点(如图2)。现向下用力压乙,当弹簧上端下降到C点时将弹簧锁定,C、A两点间的距离为△l=6.0cm。一个质量为m=0.10kg的小球丙从距离乙正上方h=0.45m处自由落下(如图3),当丙下落到位置C时,立即解除与弹簧的锁定。此后,丙与乙发生弹性碰撞(碰撞时间极短),问(1)碰撞后,乙、丙两物体的速度为多少? (2)若碰撞后取走小球丙,且已知当甲第一次刚离开地面时乙的速度为v = 2.0m/s。求从弹簧被解除锁定到至甲第一次刚离开地面时,弹簧弹性势能的改变量为多少?(g=10m/s2)w.w.^w.k.s.5*
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com