19. 解：(1)设，由，得，……2分

由得，即， ……5分

由于点P在轴的正半轴上，所以，

故点M的轨迹C的方程为()　 ……7分

(2)由得， ……9分

得，，……10分

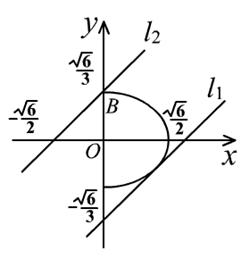
因为()表示椭圆在轴右边部分.

椭圆的上顶点，

所以数形结合得

所以的取值范围为.　　 ……14分

18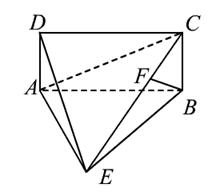．(1)证明：ABCD是矩形

BCAB

平面EAB平面ABCD，平面EAB平面ABCD=AB，BC平面ABCD

BC平面EAB　　　

EA平面EAB

BCEA　　　　 ……2分

BF平面ACE，EA平面ACE

　BF EA　　　　　 ……3分

　BC BF=B，BC平面EBC，BF平面EBC

　EA平面EBC　　　　　　　

BE平面EBC

　EA BE　　　　　　　　　　　 ……5分

(2) 　EA BE

AB=

　　 ……6分

设O为AB的中点，连结EO，

AE=EB=2

EOAB

平面EAB平面ABCD

EO平面ABCD，即EO为三棱锥E-ADC的高，且EO=　 ……8分

　　　 ……9分

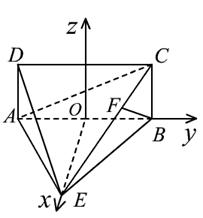(3)以O为原点，分别以OE、OB所在直线为，如图建立空间直角坐标系，则，　

　……10分

由(2)知是平面ACD的一个法向量，

设平面ECD的法向量为，则

即

令，则，所以　　 ……12分

设二面角A-CD-E的平面角的大小为，由图得，则

　　 ……13分

所以二面角A-CD-E的余弦值为　　 ……14分

若(1)、(2)问都用向量做，按步骤给分就可以.

17. 解：(1)用事件表示该同学在第个交通岗遇到红灯，

事件表示“在第一个交通岗遇到红灯，其它交通岗未遇到红灯”，……1分

则，且事件两两相互独立．　　 …………2分

所以．……4分

(2)因为该同学经过三个交通岗时，是否遇到红灯互不影响，所以可看成3次独立重复试验，

即　　　　　　 ……………………………………………………6分

所以该学生不迟到的概率为：

　　 …8分

(3)因为随机变量　　　　 ………………………9分

所以，………………………………………10分

．　 ……………………………………………11分

答：该同学恰好在第一个交通岗遇到红灯的概率为；该同学不迟到的概率为；的数学期望为1，方差为．　　　 ………………………………………12分

16.解：(1) 依题知得　 　　……3分

　也就是 ，又，所以　 ……6分

(2) ，且，所以 　　……8分

，且，…10分

所以 ， 即 　　……12分

15.(几何证明选讲选做题) 解析：连接OC，AC,则四点共圆，，通过计算得PC=，根据切割线定理得3．

14.(坐标系与参数方程选做题)略：相离．

13. 略：80.

12．解析：，由，得．

11．解析：函数在上为减函数 ，则，解得　　　 　，　 故填 ．

10．略：420．