5． 已知函数在R上满足，则曲线在点处的切线方程是　　　　　 ．

4． 定义在R上的函数f(x)满足f(x)= ，则f(2009)的值为　　　　　 ．

3．已知定义在R上的奇函数，满足,且在区间[0,2]上是增函数,则(　　　 )

A．　　　　　 B．

C． 　　　　　D．

2． 定义在R上的偶函数的部分图象如右图所示，则在上，下列函数中与的单调性不同的是(　　 )

A．　　 B．

C． 　　D．

1．函数的图象(　　 )

　 A． 关于原点对称　　　　　　　　　　 B．关于主线对称

　 C． 关于轴对称　　　　　　　　　　 D．关于直线对称

4．导数与单调性、极(最)值问题．

导数作为工具来研究三次函数、指数函数、对数函数的单调性，极值、最值时，具有其独特的优越性，要理解导数的几何意义，熟练导数的运算公式，善于借助导数解决有关的问题．

例4．已知函数，其中．

(1)当满足什么条件时，取得极值?

(2)已知，且在区间上单调递增，试用表示出的取值范围．

解析： (1)由已知得，令，得，

要取得极值，方程必须有解，

所以△，即，　 此时方程的根为：

，，

所以 w．w．w．k．s．5．u．c．o．m　 　

当时，

所以在x ₁， x₂处分别取得极大值和极小值．

当时，

所以在x ₁， x₂处分别取得极大值和极小值．

综上，当满足时，取得极值．

(2)要使在区间上单调递增，需使在上恒成立．

即恒成立，所以，

设，，

令得或(舍去)，

当时，，当时，单调增函数；

当时，单调减函数，

所以当时，取得最大，最大值为．

所以．

当时，，此时在区间恒成立，

所以在区间上单调递增，

当时最大，最大值为，所以．

综上，当时， ；当时， ．

点评：本题为三次函数，利用求导的方法研究函数的极值、单调性和函数的最值，函数在区间上为单调函数，则导函数在该区间上的符号确定，从而转为不等式恒成立，再转为函数研究最值．运用函数与方程的思想，化归思想和分类讨论的思想解答问题．

[思想方法]

[例1]若是方程的解，是 的解，则的值为(　　 )

A． 　　　B．　 　C．　 　　D．

[解析]作出的图象，交点横坐标为，而．

[答案]C

[点评]该题考查了指数函数、对数函数的图象及性质．综合了函数的图象、方程的解及曲线的交点等问题．指数函数、对数函数是两类重要的基本初等函数， 高考中以它们为载体的函数综合题既考查双基， 又考查对蕴含其中的函数思想、等价转化、分类讨论等思想方法的理解与运用．

[例2]若函数f(x)=a-x-a(a>0且a1)有两个零点，则实数a的取值范围是　　　 ．

[解析]设函数且和函数，则函数f(x)=a-x-a(a>0且a1)有两个零点， 就是函数且与函数有两个交点，由图象可知当时两函数只有一个交点，不符合，当时，因为函数的图象过点(0，1)，而直线所过的点一定在点(0，1)的上方，所以一定有两个交点．所以实数a的取值范围是．

[答案]

[点评]本题考查了指数函数的图象与直线的位置关系，隐含着对指数函数的性质的考查，根据其底数的不同取值范围而分别画出函数的图象解答．体现了对分类讨论思想的考查，分类讨论时，要注意该分类时才分类，讨论务必要全面．

[例3]已知偶函数在区间单调增加，则满足＜的x 取值范围是(　　 )

(A)(，)　　 (B) ［，)　　 (C)(，)　　 (D) ［，)

[解析]由于f(x)是偶函数，故f(x)＝f(|x|)， ∴得f(|2x－1|)＜f()，再根据f(x)的单调性，得|2x－1|＜，解得＜x＜．

[答案]B

[点评]该题的关键是将含有函数符号的不等式转化为普通的不等式，体现的对转化思想的考查，同时还综合考查了函数的性质，而该题的转化的依据就是函数的奇偶性和单调性．考题中通过这种形式来考查函数的性质与方程、不等式等的综合不但是一个热点，而且成了一个固定的必考题型．

[专题演练]

3．函数的实际应用

函数的实际运用主要是指运用函数的知识、思想和方法综合解决问题．函数描述了自然界中量的依存关系，是对问题本身的数量本质特征和制约关系的一种刻画，用联系和变化的观点提出数学对象，抽象其数学特征，建立函数关系．掌握有关函数知识是运用函数思想的前提，考生应具备用初等数学思想方法研究函数的能力，运用函数思想解决有关数学问题的意识是运用函数思想的关键．

例3．某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，如果将楼房建为x(x10)层，则每平方米的 平均建筑费用为560+48x(单位：元)．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？

(注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=)

解析：设楼房每平方米的平均综合费为元，依题意得：

．

则，令，即，解得．

当时，；当时，，

因此，当时，取得最小值，元．

答：为了使楼房每平方米的平均综合费最少，该楼房应建为15层．

点评：这是一题应用题，利用函数与导数的知识来解决问题．利用导数，求函数的单调性、求函数值域或最值是一种常用的方法．

2．函数与解方程、不等式的综合问题

函数与方程、不等式、数列是密切相关的几个部分，通过建立函数模型来解决有关他们的综合问题是高考的考查方向之一，解决该类问题要善于运用转化的思想方法，将问题进行不断转化，构建模型来解决问题．

例2．x为何值时，不等式成立．

解析：当时，．

当时，．

故时，．

时，为所求．

点评：该题考查了对数不等式的解法，其基本的解题思路为将对数不等式转化为普通不等式，需要注意转化之后的范围发生了变化，因此最后要检验，或者转化时将限制条件联立．

1．函数的性质与图象

函数的性质是高考考查的重点内容．根据函数单调性和奇偶性的定义，能判断函数的奇偶性，以及函数在某一区间的单调性，从数形结合的角度认识函数的单调性和奇偶性，掌握求函数最大值和最小值的常用方法．函数的图象是函数性质的直观载体，能够利用函数的图象归纳函数的性质．对于抽象函数一类，也要尽量画出函数的大致图象，利用数形结合讨论函数的性质．

例1．“龟兔赛跑”讲述了这样的故事：领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点……用S1、S2分别表示乌龟和兔子所行的路程，t为时间，则下图与故事情节相吻合的是(　　 )

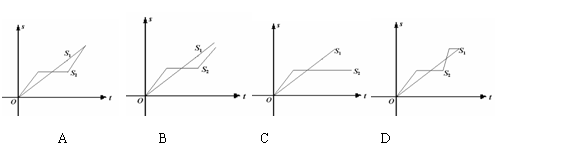
答案：B

解析：在选项B中，乌龟到达终点时，兔子在同一时间的路程比乌龟短．

点评：函数图象是近年高考的热点的试题，考查函数图象的实际应用，考查学生解决问题、分析问题的能力，在复习时应引起重视．

例2．已知定义在R上的奇函数，满足，且在区间[0,2]上是增函数，若方程f(x)=m(m>0)在区间上有四个不同的根，则

答案：-8

解析：因为定义在R上的奇函数，满足，所以，所以, 由为奇函数，所以函数图象关于直线对称且，由知，所以函数是以8为周期的周期函数，又因为在区间[0,2]上是增函数，所以在区间[-2,0]上也是增函数．如图所示，那么方程f(x)=m(m>0)在区间上有四个不同的根，不妨设_，由对称性知_，．所以_．

点评：本题综合考查了函数的奇偶性,单调性，对称性，周期性，以及由函数图象解答方程问题，运用数形结合的思想和函数与方程的思想解答问题．

2．对于函数部分考查的重点为：函数的定义域、值域、单调性、奇偶性、周期性对称性和函数的图象；指数函数、对数函数的概念、图象和性质；应用函数知识解决一些实际问题；导数的基本公式，复合函数的求导法则；可导函数的单调性与其导数的关系，求一些实际问题(一般指单峰函数)的最大值和最小值．

[知识交汇]