21．(12分)已知数列{}中，(n≥2，)，数列，满足()

　(1)求证数列{}是等差数列；

　(2)求数列{}中的最大项与最小项，并说明理由；

　(3)记…，求．

20．(12分)商学院为推进后勤社会化改革，与桃园新区商定：由该区向建设银行贷款500万元在桃园新区为学院建一栋可容纳一千人的学生公寓，工程于2002年初动工，年底竣工并交付使用，公寓管理处采用收费还贷偿还建行贷款(年利率5%，按复利计算)，公寓所收费用除去物业管理费和水电费18万元．其余部分全部在年底还建行贷款．

　(1)若公寓收费标准定为每生每年800元，问到哪一年可偿还建行全部贷款；

　(2)若公寓管理处要在2010年底把贷款全部还清，则每生每年的最低收费标准是多少元(精确到元)．(参考数据：lg1.7343＝0.2391，lgl.05＝0.0212，＝1.4774)

18．(12分)设两个向量、，满足||＝2，||＝1，、的夹角为60°，若向量与向量的夹角为钝角，求实数t的取值范围．

　注意：考生在(19甲)、(19乙)两题中选一题作答，如果两题都答，只以(19甲)计分．

19甲．(12分)如图，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB∶AD＝∶1，F是AB的中点．

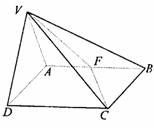
　(1)求VC与平面ABCD所成的角；

　(2)求二面角V-FC-B的度数；

　(3)当V到平面ABCD的距离是3时，求B到平面VFC的距离．

19乙．(12分)如图正方体ABCD-中，E、F、G分别是、AB、BC的中点．

　(1)证明：⊥EG；

　(2)证明：⊥平面AEG；

　(3)求，．

17．(12分)已知函数．

　(1)若x∈R，求f(x)的单调递增区间；

　(2)若x∈[0，]时，f(x)的最大值为4，求a的值，并指出这时x的值．

16．(文)同(理)第15题

　(理)已知数列{}前n项和其中b是与n无关的常数，且0＜b＜1，若存在，则________．

15．(文)在的展开式中常数项是________．

　(理)已知函数在区间(-1，1)上是增函数，则实数a的取值范围是________．

14．已知正方体ABCD－，则该正方体的体积、四棱锥-ABCD的体积以及该正方体的外接球的体积之比为________．

13．已知函数，则________．

12．将函数y＝2x的图像按向量平移后得到函数y＝2x+6的图像，给出以下四个命题：①的坐标可以是(-3.0)；②的坐标可以是(0，6)；③的坐标可以是(-3，0)或(0，6)；④的坐标可以有无数种情况，其中真命题的个数是(　)

　A．1　　　 B．2　　　C．3　　　 D．4

第Ⅱ卷(非选择题，共90分)

11．某校有6间不同的电脑室，每天晚上至少开放2间，欲求不同安排方案的种数，现有四位同学分别给出下列四个结果：①；②；③；④．其中正确的结论是(　)

　A．仅有①　　　　　　B．仅有②

　C．②和③　　　　　　D．仅有③