21．本小题满分12分

　　 已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个端点，BC过椭圆的中心O，且·＝0，｜｜＝2｜｜．

　 (Ⅰ)求椭圆的方程；

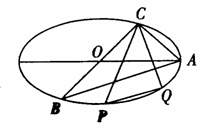　 (Ⅱ)如果椭圆上的两点P、Q使∠PCQ的平分线垂直于OA，那么是否总存在实数λ，使得＝λ?请说明理由．

20．本小题满分12分

　　 已知数列{}的前n项和为，若a₁＝2，n·＝+n(n+1)，

　 (Ⅰ)求数列{}的通项公式；

　 (Ⅱ)令T_n＝，①当n取何正整数时，>，成立；②若对一切正整数n，总有

≤m，求实数m的取值范围．

19．本小题满分12分

　　 如图，在四棱锥E－ABCD中，AB⊥平面BCE，CD⊥平面BCE，AB＝BC＝CE＝2CD＝4，∠BCE＝60°．

　 (Ⅰ)证明：平面BAE⊥平面DAE；

　 (Ⅱ)设线段AB的中点为P，求直线PE与平面DCE所　

成的角

18．本小题满分12分

　　 据统计，某大型商场一个月内被消费者投诉的次数为0，1，2的概率分别为0．4，0．5，0．1．假设一月份与二月份被消费者投诉的次数互不影响．

　 (Ⅰ)求该商场在这两个月内共被消费者投诉2次的概率；

　 (Ⅱ)求该商场在这两个月内被消费者投诉的次数ξ的分布列及其数学期望．

17．本小题满分10分　　

在直角坐标系xOy中，若角α的始边为x轴的非负半轴，终边为射线l ：y＝2x

(x≥0)．

　 (Ⅰ)求sin(α+)的值；

　 (Ⅱ)若P、Q分别是角α始边与终边上的动点，且｜PQ｜＝4，求△POQ的面积的最大值．

16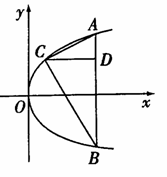．如图，Rt△ABC的三个顶点都在给定的抛物线y²＝2px

(p>0)上，斜边AB平行于y轴，则斜边上的高CD

等于___________.

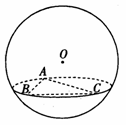
15．如图，在半径为3的球面上有A、B、C三点，∠ABC＝90°，

BA＝BC，球心O到平面ABC的距离是，则B、C两点

间的球面距离是____________.

14．2010年上海世博会组委会分配甲、乙、丙、丁四人做三项工作，每一项工作至少分一人，且甲、乙两人不能同时做同一项工作，则不同的分配种数是_____________(用数字作答)．

13．的二项展开式中项的系数为___________(用数字作答).

12．已知函数f(x)是定义在R上的不恒为0的函数，且对于任意实数a、b满足f(ab)＝af(b)+bf(a),f(2)＝2,　 ＝(n∈N﹡),　 ＝ (n∈N﹡)．

　　 考察下列结论：①f(0)＝f(1)；②f(x)为奇函数；③数列{}为等差数列；④数列{}为等比数列．其中正确的个数为

A．1　 　　　　　B．2 　　　　　　　C．3 　　　　　　　D．4

第Ⅱ卷