2．解析：由，得=1,或2，选C．

ACCB　　 BDCD

1．解析： ,　 选A．

21. (本题满分14分)已知正项数列中，，点在抛物线上；数列中，点在直线上.

(1)求数列，的通项公式；

(2)若问是否存在，使成立，若存在，求出值；若不存在，说明理由；

(3)对任意正整数，不等式恒成立，求正实数的取值范围.

数学(理科)评分标准

20．(本题满分14分)已知，其中是无理数，且，

(1)当时, 求的单调区间、极值；

(2)求证：在(1)的条件下，；

(3)是否存在实数，使的最小值是，若存在，求出的值；若不存在，说明理由.

19.(本题满分14分)已知点R(-3，0)，点P在轴的正半轴上，

点Q在轴上，点M在直线PQ上，且满足

．

(1)求点M的轨迹C的方程；

(2)设直线与曲线C恒有公共点，

求的取值范围.

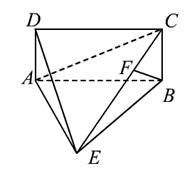
18．(本题满分14分)如图，四棱锥E-ABCD中，ABCD是

矩形，平面EAB平面ABCD,AE=EB=BC=2,F为CE上的点，

且BF平面ACE．

(1)求证：AEBE；

(2)求三棱锥D-AEC的体积；

(3)求二面角A-CD-E的余弦值．

17. (本题满分12分) 已知某同学上学途中必须经过三个交通岗，且在每一个交通岗遇到红灯的概率均为，假设他在3个交通岗遇到红灯的事件是相互独立的,用随机变量表示该同学遇到红灯的次数．

(1)求该同学在第一个交通岗遇到红灯，其它交通岗未遇到红灯的概率；

(2)若，则该同学就迟到，求该同学不迟到的概率；

(3)求随机变量的数学期望和方差．

16.(本题满分12分)在中，分别为角的对边．已知 ，，且.

(1) 求角；

(2) 若，的面积，求的值.

(二)选做题(14~15题，考生只能从中选做一题，两道题都做的，只记第一题的分.)

14.(坐标系与参数方程选做题)已知曲线，

曲线(t为参数)，则与的位置关系为________.

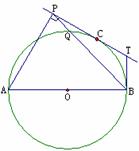
15.(几何证明选讲选做题)如图，AB为的直径，C为上一点，

AP和过C的切线互相垂直，垂足为P，过B的切线交过C的切线于T，

PB交于Q，若，AB=4，则　　　　　 　.

(一)必做题(9~13题)

9．经过两条直线的交点，

且与直线平行的直线一般式方程为　　　　 　．

10．如果执行右侧的程序框图，那么输出的　　　 ．

11．若函数在上为减函数，则实数a的取值范围是　　　　 　．

12．的展开式中的第3项含有，则的值为　　　 　　．

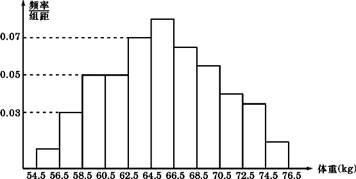
13.为了了解某地区高三学生的身体发育情况，抽查该地区200名年龄为17.5岁－18岁的男生体重(kg) ,得到频率分布直方图如下，根据下图可得这200名学生中体重在的学生人数是_____　 ．