
3.反应向右进行,平衡向左移动。理由:增大反应物的浓度,正反应速率增大,此时逆反应速率不变,所以,反应向正反应方向进行。由于,新加入的PCl5的转化率比原来容器中的低(原理分析同1),所以,平衡向左移动了。
下面说明一下,以上观点的错误原因:
观点一:把平衡后再充入1mol PCl5的过程,同开始就充入2 mol PCl5等价,本身犯了“偷换概念”的错误。即使等价于开始充入2 mol PCl5,也不能称之为平衡的移动,平衡的移动是指对于同一容器中的达到平衡的可逆反应,因条件改变而引起的变化。
观点二:不能把平衡移动的方向和物质的百分含量联系在一起。如:在一定温度下,某密闭容器中进行合成氨的反应N2+3H2 2NH3达到平衡,再充入n
mol H2平衡向右移动,达新平衡后NH3的百分含量增大吗?很明显,不一定,这取决于n与原来平衡混合气的总物质的量的大小对比(主要)和反应进行的程度;如:n远大于原平衡混合气的总物质的量时,氨气的百分含量一定减小了。所以,化学平衡移动的方向与物质的百分含量无关。
2NH3达到平衡,再充入n
mol H2平衡向右移动,达新平衡后NH3的百分含量增大吗?很明显,不一定,这取决于n与原来平衡混合气的总物质的量的大小对比(主要)和反应进行的程度;如:n远大于原平衡混合气的总物质的量时,氨气的百分含量一定减小了。所以,化学平衡移动的方向与物质的百分含量无关。
观点三:好象很圆滑,但也犯了将平衡移动方向和反应物的转化率混为一谈的错误。认为转化率提高平衡就向右移动,反之向左移动,本身就是错误的。举例说明:一定温度下,在一体积固定的密闭容器中,加入1 mol H2和1 mol I2(g),达到平衡后,充入1 mol H2则平衡向右移动,再充入1 mol I2(g)平衡又向右移动,但根据转化率的关系,因为首次平衡和最终平衡态的转化率相等,就会得出两次右移等于平衡不移动的谬论。
产生以上错误的根本原因在于没有弄清楚,平衡移动的判断标准,化学平衡的移动是旧的平衡被破坏,建立新平衡的过程,旧的平衡被破坏的原因是v(正)=v(逆)的条件被打破,从而产生两种平衡移动的方向,v(正)′> v(逆)′平衡右移,v(正)′< v(逆)′平衡左移。
综上所述,化学平衡移动的标准是:改变外界条件后v(正)′和v(逆)′的大小关系,若v(正)′> v(逆)′则平衡右移,若v(正)′< v(逆)′则平衡左移,或者说是和反应进行的方向一致。
对教材的建议:
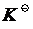
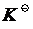
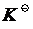 1、大学教材中,化学平衡移动的判断依据是:反应商(Q)与标准平衡常数( )的相对大小的变化,平衡时Q= ,改变条件使Q< ,平衡被破坏,反应向正向(或逆向)进行,之后重新建立平衡,我们说平衡右移(左移)
1、大学教材中,化学平衡移动的判断依据是:反应商(Q)与标准平衡常数( )的相对大小的变化,平衡时Q= ,改变条件使Q< ,平衡被破坏,反应向正向(或逆向)进行,之后重新建立平衡,我们说平衡右移(左移)
1.平衡向左移动了。理由:再向容器中加入1 mol PCl5,和开始加入2 mol PCl5达到平衡时的效果一样。容积固定的密闭容器中,成比例的增大反应物的量,相当于加压过程(图示中乙容器充了2 mol PCl5,等价于丙容器充入2 mol PCl5达到平衡后,将活塞从B推至A处),所以加压平衡向左进行。
 2.平衡向左移动。理由:达到新平衡时,加入的PCl5未转化的更多了,容器中PCl5的百分含量比原来容器中的高(原理分析同1),所以,平衡向左移动了。
2.平衡向左移动。理由:达到新平衡时,加入的PCl5未转化的更多了,容器中PCl5的百分含量比原来容器中的高(原理分析同1),所以,平衡向左移动了。
21.已知过点A(-4,0)的动直线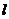 与抛物线
与抛物线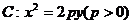 相交于B、C两点。当
相交于B、C两点。当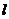 的斜率是
的斜率是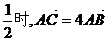 。
。
(1)求抛物线C的方程;
(2)设BC的中垂线在y轴上的截距为b,求b的取值范围。
福建省宁德市2010年高中毕业班教学质量检查
20.已知函数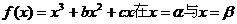 处有两上不同的极值点,设
处有两上不同的极值点,设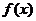 在点
在点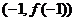 处切线为
处切线为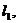 其斜率为
其斜率为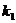 ;在点
;在点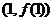 利的切线为
利的切线为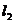 ,其斜率为
,其斜率为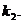
(1)若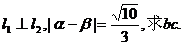
(2)若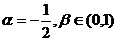 ,求
,求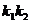 的取值范围。
的取值范围。
18.已知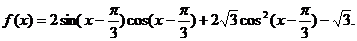
(1)求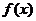 的最大值及取得最大值时相应的x的值;
的最大值及取得最大值时相应的x的值;
(2)若函数 上恰有两上零点
上恰有两上零点 的值。
的值。
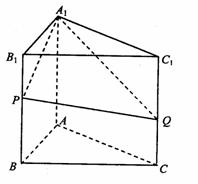 19.如图,三棱柱ABC-A1B1C1,侧棱与底面垂直,AB=AC=1,AA1=2,P、Q、M分别是棱BB1、CC1、B1C1的中点,AB⊥AQ。
19.如图,三棱柱ABC-A1B1C1,侧棱与底面垂直,AB=AC=1,AA1=2,P、Q、M分别是棱BB1、CC1、B1C1的中点,AB⊥AQ。
(1)求证:AC⊥A1P;
(2)求证:AQ//面A1PM;
(3)求AQ与面BCC1B1所成角的大小。
17.已知数列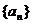 前n项和
前n项和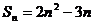 ,数列
,数列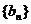 是各项为正的等比数列,满足
是各项为正的等比数列,满足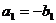 ,
,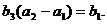
(1)求数列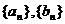 的通项公式;
的通项公式;
(2)记 的最大值。
的最大值。
16. 若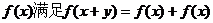 ,则可写出满足条件的一个函数解析式
,则可写出满足条件的一个函数解析式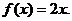 类比可以得到:若定义在R上的函数
类比可以得到:若定义在R上的函数
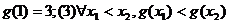 ,则可以写出满足以上性质的一个函数解析式为
,则可以写出满足以上性质的一个函数解析式为
。
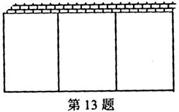
15.有一批材料可以建成200m长的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样材料同成三个面积相等的矩形(如图所示),则围成场地的最大面积
为 (围墙厚度不计)
14.数列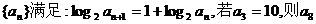 = 。
= 。
13.若 的最小值为
。
的最小值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com