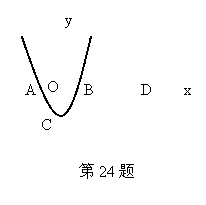
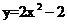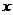24．如图，已知二次函数的图像与轴交于A、B两点(A在点B的左边)，与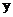轴交于点C，直线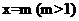与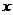轴交于点D。

(1)求A、B、C三点的坐标；

(2)在直线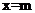()上有一点P(点P在第一象限)，使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求P点的坐标；(用含m的代数式表示)。

(3)在(2)成立的条件下，试问：抛物线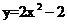上是否存在一点Q，使得四边形ABPQ为平行四边形？如果存在这样的点Q，请求出m的值；如果不存在，请简要说明理由。

23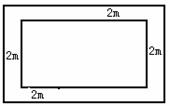．某学校打算在校园里划分一块矩形空地进行绿化，要求在中央布置一个长比宽多4米的矩形(即图中小矩形)花坛，四周铺植2米宽的草地，现甲、乙两位同学分别提出如下两个设想：

甲：中央矩形花坛面积要为45平方米；

乙：草地总面积要为32平方米；

问这两位同学的设想分别能实施吗？若能，试求划出的这块矩形(即图中大矩形)空地的长和宽；若不能，试说明理由.

22．如图，PA、PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=70°．求∠P的度数．

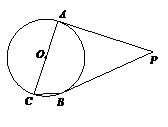
21．如图,△ABC和△DEF在平面直角坐标系中的位置如图所示．

　 　(1)将△ABC向下平移1个单位得到△A₁B₁C₁，请画出△A₁B₁C₁；并写出点A的对应点A₁的坐标；

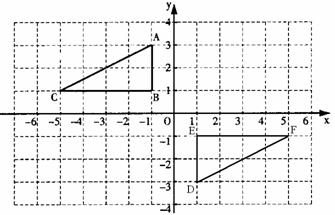(2)能否将△A₁B₁C₁通过旋转变换得到△DEF?若能试作出旋转中心,并求出旋转角，若不能说明理由.

20．小明和小慧玩纸牌游戏．下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小明先从中抽出一张，小慧从剩余的3张牌中也抽出一张．

小慧说：若抽出的两张牌的数字都是偶数，你获胜；否则，我获胜．

(1)请用树状图表示出两人抽牌可能出现的所有结果；

(2)若按小慧说规则进行游戏，这个游戏公平吗？请说明理由．

19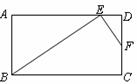．如图，在矩形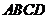中，点分别在边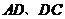上，BE⊥EF，AB=6cm，AD=11cm(其中AE＞DE)，DF=4cm，求BE的长．

18．已知a、b、c分别是△ABC的三边，其中a＝1，c＝4，且关于x的方程有两个相 等的实数根，试判断△ABC的形状。

17．化简:.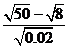　　　　　　　　

16．如图，在已建立直角坐标系的4×4的正方形方格纸中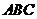，△是格点三角形(三角形的三个顶点都是小正方形的顶点)， 若以格点、、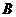为顶点的三角形与△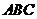相似(C点除外)，则格点的坐标是　　　　

15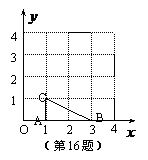．如图⊙和⊙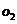外切,它们的半径分别为1和2,过O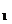作⊙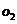的切线,切点为A,则O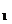A长为　　　　　 .