4.　 All of a sudden, a man who held a gun knocked down an old woman and took her

bag, __________ round the corner.

A. disappeared　　 　　　　　　　　　　　　　　 B. disappearing　　

C. having disappeared　 　　　　　　　　　 D. to disappear

3.　 The idea puzzled me so much that I stopped for a few seconds to try to _______.

A. make it out　 　　　 B. make it off　 C. make it up 　　　　　 D. make it over

2.　 He hasn’t slept at all for three days. _______ he is tired out.

A. There is no point　　 　　　　　　　　 B. There is no need　 　　

C. It is no wonder　 　　　　　　　　　　　　 D. It is no way

第一节 单项填空(共15小题;每小题1分，满分15分)

从A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

1.　 I knew ______ John Lennon, but not ______ famous one.

A. / ；a　 　　　　 B. a ；the　　 　　 C. / ；the　 　　　　　　　　　　 D. the ；a

25．(本小题满分8分)

已知抛物线的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C(0，3)，过点C作x轴的平行线与抛物线交于点D，抛物线的顶点为M，直线y= x+5经过D、M两点.

(1)求此抛物线的解析式；

(2)连接AM、AC、BC，试比较∠MAB和∠ACB的大小，并说明你的理由.

解：(1)

24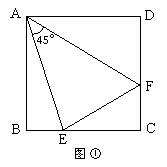．(本小题满分7分)

如图①，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45 °，则有结论EF＝BE+FD成立；

(1)如图②，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是BC、CD上的点，且∠EAF是∠BAD的一半，那么结论EF＝BE+FD是否仍然成立？若成立，请证明；若不成立，请说明理由；

解：

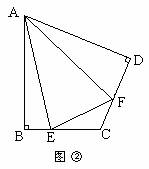
(2)若将(1)中的条件改为：在四边形ABCD中，AB＝AD，∠B+∠D＝180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF＝BE+FD是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.

解：

23．(本小题满分7分)

我们给出如下定义：若一个四边形中存在一组对边的平方和等于另一组对边的平方和，则称这个四边形为等平方和四边形．

(1)写出一个你所学过的特殊四边形中是等平方和四边形的图形的

名称：　　　　　　　 ．

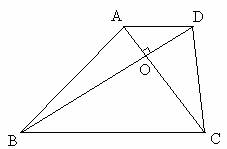(2)如图(1)，在梯形ABCD中，AD∥BC，

AC⊥BD，垂足为O．

求证：，即四边形ABCD是等平方和四边形．

证明：

图(1)　　　　　　　　　　　　　 　　

(3)如果将图(1)中的△AOD绕点O按逆时针方向旋转α度(0<α<90)后得到图(2)，那么四边形ABCD能否成为等平方和四边形？若能，请你证明；若不能，请说明理由．

证明：

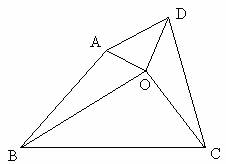
图(2)

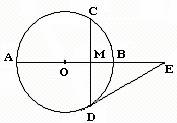
22．(本小题满分5分)

已知：如图，在⊙O中，弦CD垂直直径AB，垂足为M，AB=4，CD=，点E在AB的延长线上，且.

(1)求证：DE是⊙O的切线；

(2)将△ODE平移，平移后所得的三角形记为△．求当点与点C重合时，△与⊙O重合部分的面积．

解：(1)

(2)

21．(本小题满分5分)

已知a、b是关于x的一元二次方程的两个实数根，其中k为非负整数，点A(a，b)是一次函数y＝(k－2)x+m与反比例函数图象的交点，且m、n为常数．

(1)求k的值；

(2)求一次函数与反比例函数的解析式．

解：(1)

(2)

20．(本小题满分5分)

如图，在矩形ABCD中，AD=8，AB=6，点A处有一动点E以1/的速度由A向B运动，同时点C处也有一动点F以2/的速度由C向D运动，设运动的时间为，四边形EBFD的面积为，求与的函数关系式及自变量的取值范围.

解：