
21.解:(Ⅰ)依题意,可知

解得 ……3分
……3分
 椭圆的方程为
椭圆的方程为 ……4分
……4分
(Ⅱ)直线 与⊙
与⊙ 相切
相切
则 ,即
,即 ,……5分
,……5分
 由
由 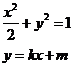 ,得
,得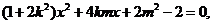 ……6分
……6分
 直线
直线 与椭圆交于不同的两点
与椭圆交于不同的两点 。设
。设

 ……7分
……7分

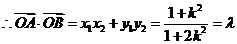 ……9分
……9分

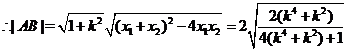 ……10分
……10分
设
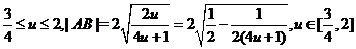
 在
在 上单调递增
上单调递增  ……12分
……12分
20.解:(Ⅰ)  ……2分
……2分
 当
当 时,
时,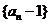 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列
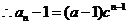 ,即
,即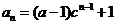 ……4分
……4分
当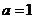 时,
时,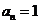 仍满足上式。
仍满足上式。
 数列
数列 通项公式为
通项公式为 ……6分
……6分
(Ⅱ)由(Ⅰ)得,当 时,
时,
 ……8分
……8分


两式作差得

 ……12分
……12分
19.(本题满分12分)
解:(Ⅰ)在梯形 中,
中, ,得
,得

又 ,故△
,故△ 为等腰直角三角形。
为等腰直角三角形。 …2分
…2分
连接 ,交
,交 于点
于点 ,则
,则 ……3分
……3分
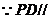 平面
平面 ,又平面
,又平面 平面
平面
在△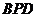 中,
中, ……5分
……5分
即 时,
时, 平面
平面 ………6分
………6分
(Ⅱ)方法一:在等腰直角△ 中,取
中,取 中点
中点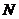 ,连结
,连结 ,则
,则
 平面
平面 平面
平面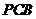 ,且平面
,且平面 平面
平面 平面
平面
在平面 内,过
内,过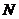 作
作 直线
直线 于
于
 连结
连结 ,由
,由
得 平面
平面 ,故
,故
 就是二面角
就是二面角 的平面角……8分
的平面角……8分
在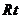 △
△ 中,设
中,设
则
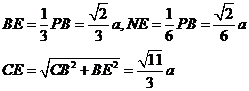
由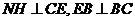 可知:△
可知:△ ∽△
∽△
代入解得: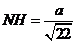 。在
。在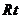 △
△ 中,
中,
 ………11分
………11分
 二面角
二面角 的余弦值为
的余弦值为 ………12分
………12分
方法二:以 为原点,
为原点, 所在直线分别为
所在直线分别为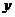 轴、
轴、 轴,如图建立空间直角坐标系。
轴,如图建立空间直角坐标系。
 设
设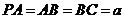 ,则
,则 ……7分
……7分
设 为平面
为平面 的一个法向量,
的一个法向量,
 则
则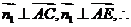

解得 ……9分
……9分
设 为平面
为平面 的一个法向量,则
的一个法向量,则
 又
又
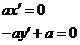 ,解得
,解得
 ……11分
……11分
 二面角
二面角 的余弦值为
的余弦值为 ……12分
……12分
18.解:(1)  的取值为
的取值为
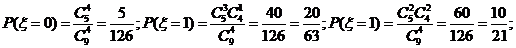
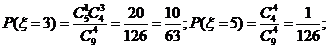 ………4分
………4分
 的分布列为:
的分布列为:



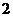








 ………7分
………7分
(2)  ………8分
………8分
 ………9分
………9分
 ………10分
………10分
 要使
要使 的最大值为
的最大值为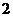 。………12分
。………12分
17.解:(Ⅰ)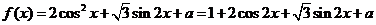 ………2分
………2分
 ………4分
………4分
因为
所以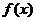 的最小值为
的最小值为 ,由题意
,由题意 ………7分
………7分
(Ⅱ) 
令 ,则
,则 ………9分
………9分
令 ,则
,则
当 ,当
,当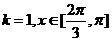
所以函数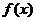 在
在 上的单调增区间为
上的单调增区间为 和
和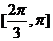 ………12分
………12分
13.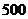 ; 14.
; 14. ; 15.
; 15. ; 16.
; 16.
C B A D C B D C A B B C
22.(本小题满分14分)
已知函数 。
。
(Ⅰ)若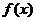 在
在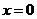 处取得极值,求
处取得极值,求 的值;
的值;
(Ⅱ)讨论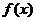 的单调性;
的单调性;
(Ⅲ)当 时,证明:
时,证明: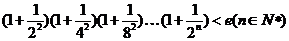 。
。
09-10学年第二学段诊断性检测
高 三 数 学(理)
20.(本小题满分12分)
设数列 满足
满足 ,其中
,其中 为实数,且
为实数,且 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和为
项和为 。
。
2l.(本小题满分12分)
已知 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为坐标原点,点
为坐标原点,点 在椭圆上,且
在椭圆上,且 ,⊙
,⊙ 是以
是以 为直径的圆,直线
为直径的圆,直线 与⊙
与⊙ 相切,并且与椭圆交于不同的两点
相切,并且与椭圆交于不同的两点 。
。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当 ,且满足
,且满足 时,求弦长
时,求弦长 的取值范围。
的取值范围。
19.(本小题满分12分)
 如图,四棱锥
如图,四棱锥 中,
中, 底面
底面 ,底面
,底面 为梯形,
为梯形,

 ,且
,且 ,点
,点 是棱
是棱 上的动点。
上的动点。
(Ⅰ)当 平面
平面 时,确定点
时,确定点 在棱
在棱 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角 的余弦值。
的余弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com