
5.在横线处填人语句,顺序最恰当的一项是 ( )
胡同是北京特有的一种古老的城市小巷, , 。 。 ,
。
①明清以后又不断发展,最多时有6000多条
②这些地区都是您感受胡同文化的好去处
③据统计,北京现有胡同1000多条,纵横交错,织成了荟萃万千的老北京景观
④现今胡同景观保存相对完好的区域有东城区、西城区和前门地区
⑤北京胡同最早起源于元代
A.④②⑤①③ B.④②③⑤①
C.⑤④①②③ D.⑤①③④②
4.与下列文学常识的表述,对应正确的一项是 ( )
①他,头戴峨冠,身佩兰草,徜徉在汨罗江畔,为民生多艰“长太息”,当国家衰亡之时,仍以纵身一跃坚守着理想。
②他,少年从戎,立志报国,跃马于大江南北,为收复中原而“挑灯看剑”,抒写理想抱负,以豪放词风闻名词坛。
③他,是中国古典戏剧的标志性人物,擅长一种把歌曲、宾白、舞蹈结合起来的艺术形式,一曲《滚绣球》感动古今。
④他,善于用十四行诗抒写人性,是英国文艺复兴时期伟大的戏剧天才 ,创造的丹麦王子哈姆雷特的形象脍炙人口。
,创造的丹麦王子哈姆雷特的形象脍炙人口。
A.①屈原 ②陆游 ③马致远 ④莎士比亚
B.①宋玉 ②辛弃疾 ③马致远 ④巴尔扎克
C.①屈原 ②辛弃疾 ③关汉卿 ④莎士比亚
D.①宋玉 ②陆游 ③关汉卿 ④巴尔扎克
3.下列句子中,没有语病的一句是 ( )
A.多年来,红桥市场凭借丰富的商品、可靠的质量、合理的价格、周到的服务 吸引了大量顾客,其中有20%是国际友人慕名前来。
吸引了大量顾客,其中有20%是国际友人慕名前来。
B.未来五年内,所有公共交通设施将配备红十字急救箱,并对司乘人员进行急救知识培训,以有效增强公 共交通设施的安全。
共交通设施的安全。
C.艺术团将传统表演与现代舞台科技相结合,大胆创作出一批符合当代观众欣赏的节目,使皮影戏这一古老剧种焕发了青春。
D.西方国家对孔子学说并不陌生,早在西方启蒙运动时期,中国的许多古代哲学思想,特别是孔子思想,就已通过传教士传到西方。
2.下列句子中,加点成语使用不恰当的一句是 ( )
A.“家电下乡”政策的出台,为正处于寒冬之中的国内家电企业吹来暖风,各大厂商为抢占商机纷纷使出浑身解数。
B.足协方面对可能出现的给中超联赛造成冲击的意外情况,已经准备好了多套应对的方案,以备不时之需。
C.涂鸦绘画在中国一直被视作地下艺术,而北京地铁四号线却能以开放的姿态让涂鸦从地下走出,使之登堂入室。
D.借助某些营销手段来提升客户的忠诚度,这只是干权宜之计,中国电信实在需要完善整个业务体系,通过服务赢得客户。
1.下列词语中,字形和加点字的读音全都正确的一项是 ( )
A.木讷 芸芸众生 参与(yǔ) 曲(qū)径通幽
B.揶揄 高潮迭起 包扎(zā) 少安毋(wú)躁
C.沉缅 四季常青 笃(dǔ)信 叱咤(zhà)风云
D.辐射 凤毛鳞角 粗犷(guǎng) 通缉(jī)罪犯
22.解:(Ⅰ)f'(x)= =
=
 ,
,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设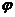 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:

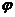 (1)=1-a-2≤0,
(1)=1-a-2≤0,
① 
 -1≤a≤1,
-1≤a≤1,
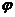 (-1)=1+a-2≤0.
(-1)=1+a-2≤0.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
方法二:


 ≥0,
≥0,
 <0,
<0,
① 或
或
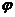 (-1)=1+a-2≤0
(-1)=1+a-2≤0
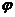 (1)=1-a-2≤0
(1)=1-a-2≤0
 0≤a≤1
或 -1≤a≤0
0≤a≤1
或 -1≤a≤0
 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由 =
=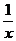 ,得x2-ax-2=0, ∵△=a2+8>0
,得x2-ax-2=0, ∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根,
x1+x2=a,x1x2=-2,
∴ 从而|x1-x2|= =
= .
.
∵-1≤a≤1,∴|x1-x2|= ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
 g(-1)=m2-m-2≥0,
g(-1)=m2-m-2≥0,
② g(1)=m2+m-2≥0,
 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;
当m≠0时,

 m>0,
m<0,
m>0,
m<0,
② 或
或
g(-1)=m2-m-2≥0 g(1)=m2+m-2≥0
 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
21.(1)设 .
.
由抛物线定义,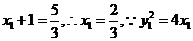 ,
,
 .
.
 在
在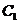 上,
上, ,又
,又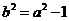

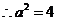 或
或 舍去.
舍去.

∴椭圆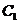 的方程为
的方程为 .
.
(2)∵直线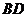 的方程为
的方程为 为菱形,
为菱形,
 ,设直线
,设直线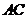 的方程为
的方程为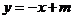
 、
、 在椭圆
在椭圆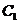 上,
上,
 .
.
设 ,则
,则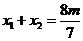 .
.
 .
.
 的中点坐标为
的中点坐标为 ,由
,由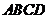 为菱形可知,点
为菱形可知,点 在直线
在直线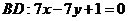 上,
上,


∴直线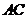 的方程为
的方程为 ,即
,即 .
.
20.解:(1)由题设 ,即
,即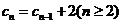
易知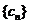 是首项为
是首项为 、公差为2的等差数列,
、公差为2的等差数列,
∴通项公式为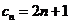 ,
,
(2)由题设, ,得
,得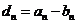 是以
是以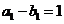 公比为
公比为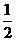 的等比数列.
的等比数列.
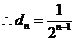
由 得
得 .
.
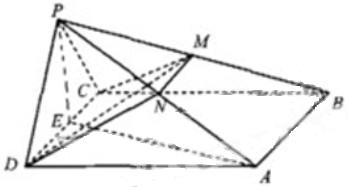
19.(1)过 作
作 于
于 连接
连接
 侧面
侧面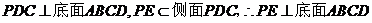
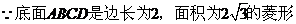 。
。

 故
故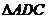 是边长为2的等边三角形。又
是边长为2的等边三角形。又 点,
点,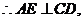 又
又 是
是 在底面
在底面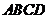 上的射影,
上的射影,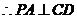
(法一)(2)
 就是二面角
就是二面角 的平面角,
的平面角, 和
和 都是边长为2的正三角形,
都是边长为2的正三角形,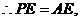 又
又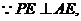
 即二面角
即二面角 的大小为45°
的大小为45°
(3)取 的中点为
的中点为 连接
连接 又
又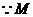 为
为 的中点,
的中点, ,又
,又 ,且
,且 在平面
在平面 上,又
上,又 为
为 的中点,
的中点, 又
又
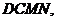
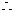 线段
线段 的长就是
的长就是 到平面
到平面 的距离在等腰直角三角形
的距离在等腰直角三角形 中,
中, ,
,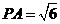 ,
,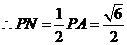 ,即
,即 到平面
到平面 的距离是
的距离是
18.解:(1)由已知条件得
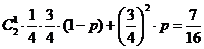
即 ,则
,则
答: 的值为
的值为 .
.
(2)解: 可能的取值为0,1,2,3
可能的取值为0,1,2,3

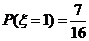
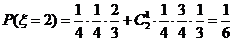

 的分布列为:
的分布列为:
 |
0 |
1 |
2 |
3 |
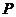 |
 |
 |
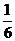 |
 |
所以
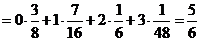
答:数学期望为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com