14. 地位于甲、乙两条河流的交汇处，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作，为了保护设备，施工部门提出以下三种方案：

方案1：运走设备，此时需花费4000元；

方案2：建一保护围墙，需花费1000元，但围墙只能抵御一个河流发生的洪水，当两河流同时发生洪水时，设备仍将受损，损失约56 000元；

方案3：不采取措施，此时，当两河流都发生洪水时损失达60000元，只有一条河流发生洪水时，损失为10000元.

(1)试求方案3中损失费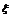(随机变量)的分布列；

(2)试比较哪一种方案好.

13. 某篮球队与其他6支篮球队依次进行6场比赛，每场均决出胜负，设这支篮球队与其他篮球队比赛胜场的事件是独立的，并且胜场的概率是.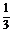

(1)求这支篮球队首次胜场前已经负了两场的概率；

(2)求这支篮球队在6场比赛中恰好胜了3场的概率；

(3)求这支篮球队在6场比赛中胜场数的期望和方差.

12．假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料，若由资料知y对x呈线性相关关系。试求：

(1)线性回归方程=bx+a的回归系数a，b；　

(2)估计使用年限为10年时，维修费用是多少？

11. 一个袋中装有大小相同的黑球、白球和红球，已知袋中共有10个球，从中任意摸出1个球，得到黑球的概率是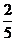;从中任意摸出2个球，至少得到1个白球的概率是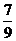.求：

　　 (1)从中任意摸出2个球，得到的数是黑球的概率；

(2)袋中白球的个数。

10. 甲、乙、丙、丁四位同学各自对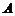、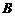两变量的线性相关性作试验，并用回归分析方法分别求得相关系数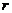与残差平方和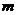如下表：

	甲	乙	丙	丁
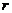	0.82	0.78	0.69	0.85
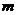	115	106	124	103

则______同学的试验结果体现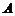、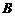两变量更强的线性相关性.

9. 某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测，若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是　　　　　　　

8. 在某项测量中，测量结果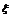服从正态分布N(1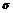，)(＞0).若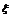在(0，1)内取值的概率为0.4，则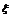在(2，+∞)上取值的概率为　 　　　　.

7. 根据下表计算

则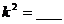

6. 从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .

5. 下图a是某县参加2009年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A₁、A₂、…、A_m [如A₂表示身高(单位：cm)在[150，155]内的学生人数]。图b是统计图a中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160-180cm(含160cm，不含180cm)的学生人数，那么在流程图中的判断框内应填写的条件是　　　　　

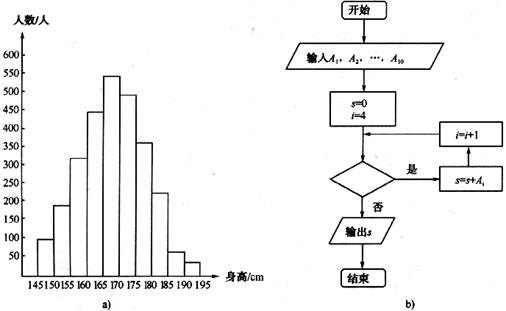
A．<9　 　　　　　　　　　　 B．<8　　　　　　　　 C．<7 　　　　　　　 D．<6